如圖，點F在□ABCD的對角線AC上，過點F、 B分別作AB、
AC的平行線相交于點E，連接BF，∠ABF=∠FBC+∠FCB．
（1）求證：四邊形ABEF是菱形；
（2）若BE=5，AD=8，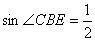
，求AC的長.
（1）證明：∵EF∥AB，BE∥AF，
∴四邊形ABEF是平行四邊形．
∵∠ABF=∠
FBC＋∠FCB，∠AFB=∠FBC＋∠FCB，
∴∠ABF=∠AFB． …………………………………………………………………1分
∴AB＝AF.
∴□ABEF是菱形． ………………………………………………………………2分
（2）解：作DH⊥AC于點H，
∵
，
∴
.
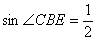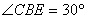∵BE∥AC，
∴
.
∵AD∥BC，
∴
.
∴
.
Rt△ADH中，
.………………………………………………3分
.
∵四邊形ABEF是菱形，
∴CD= AB=BE=5，
Rt△CDH中，
. ………………………………………………4分
∴
.……………………………………
……5分
科目：初中數學 來源： 題型：
如圖，將一個長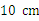為
，寬為
的矩形紙片先按照從左向右對折，再按照從下向上的方向對折，沿所得矩形兩鄰邊中點的連線（虛線）剪下（如圖（1）），再打開，得到如圖（2）所示的小菱形的面積為（ ）
A.
B.
C.
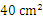D.
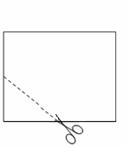
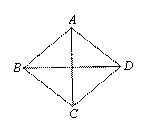
（1） （2）
查看答案和解析>>
科目：初中數學 來源： 題型：
在一個不透明的布袋里裝有4個完全相同的標有數字1、2、3、4的小球. 小明從布袋里隨機取出一個小球，記下數字為x，小紅從布袋里剩下的小球中隨機取出一個
，記下數字為y. 計算由x、y確定的點（x，y）在函數y＝－x＋5的圖象上的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
數學活動課上，老師提出這樣一個問題:如果AB=BC,∠ABC=60°,∠APC=30°,連接
PB，那么PA、PB、PC之間會有怎樣的等量關系呢？
經過思考后，部分同學進行了如下的交流：
小蕾：我將圖形進行了特殊化，讓點P在BA延長線上（如圖1），得到了一個猜想:
PA2+PC2=PB2 .
小東：我假設點P在∠ABC的內部，根據題目條件，這個圖形具有“共端點等線段”的特點，可以利用旋轉解決問題，旋轉△PAB 后得到△P′CB ,并且可推出△PBP′ ,△PCP′ 分別是等邊三角形、直角三角形，就能得到猜想和證明方法.
這時老師對同學們說，請大家完成以下問題：
（1）如圖2，點P在∠ABC的內部，
①PA=4，PC=
，PB= .
②用等式表示PA、PB、PC之間的數量關系，并證明.
（2）對于點P的其他位置，是否始終具有②中的結論？若是，請證明；若不是，請舉例說明.
|
|
查看答案和解析>>
科目：初中數學 來源： 題型：
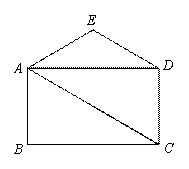
如圖，四邊形ABCD為矩形，DE∥AC，且DE=AB，過點E作AD的垂線交AC于點F．
（1）依題意補全圖，并證明四邊形EFCD是菱形；
（2）若AB=3，BC=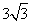
，求平行線DE與AC間的距離．
 |
查看答案和解析>>
科目：初中數學 來源：2014-2015學年福建省七年級上學期期末考試數學試卷（解析版） 題型：填空題
某商場在慶“國慶”促銷活動中，對顧客實行優惠，規定如下：
（1）若一次購物不超過100元，則不予優惠；
（2）若一次購物超過100元，但不超過300元的，則按標價給予九折優惠；
（3）若一次購物超過300元的，其中300元九折優惠，超過300元的部分則給予八折優惠。
某人兩次購物，分別付款99元與216元，若他只去一次，購買同樣的商品，則應付___________元．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的值為0，則x的值為 ．
．
米，則扇形OAB的面積為
平方米 B. 
平方米 
平方米 D. 
平方米