
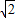 ,你能求出AG、MN的長嗎?
,你能求出AG、MN的長嗎?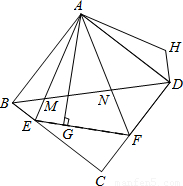
 探究一:證明:如圖,∵AG⊥EF,
探究一:證明:如圖,∵AG⊥EF,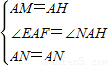 ,
,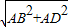 =12
=12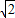 ,
,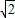 ,
, -3
-3 =9
=9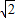 ,
,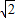 -y)2+(3
-y)2+(3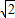 )2,解得y=5
)2,解得y=5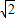 ,即MN=5
,即MN=5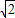 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
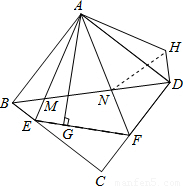
 如圖,△AEF中,∠EAF=45°,AG⊥EF于點G,現將△AEG沿AE折疊得到△AEB,將△AFG沿AF折疊得到△AFD,延長BE和DF相交于點C.
如圖,△AEF中,∠EAF=45°,AG⊥EF于點G,現將△AEG沿AE折疊得到△AEB,將△AFG沿AF折疊得到△AFD,延長BE和DF相交于點C.| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•德慶縣二模)如圖,△AEF中,∠EAF=45°,AG⊥EF于點G,現將△AEG沿AE折疊得到△AEB,將△AFG沿AF折疊得到△AFD,延長BE和DF相交于點C.
(2013•德慶縣二模)如圖,△AEF中,∠EAF=45°,AG⊥EF于點G,現將△AEG沿AE折疊得到△AEB,將△AFG沿AF折疊得到△AFD,延長BE和DF相交于點C.| 2 |
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省鹽城市東臺市聯誼學校九年級(上)期中數學試卷(解析版) 題型:解答題
 ,求AG、MN的長.
,求AG、MN的長.
查看答案和解析>>
科目:初中數學 來源:2013年江蘇省鹽城市射陽縣特庸中學中考數學一模試卷(解析版) 題型:解答題
 ,求AG、MN的長.
,求AG、MN的長.
查看答案和解析>>
科目:初中數學 來源:2012年江蘇省鹽城市中考適應性訓練數學試卷(解析版) 題型:解答題
 ,求AG、MN的長.
,求AG、MN的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com