Question

1．如圖，在平面直角坐標系xOy中，拋物線y=ax²-8ax+b交y軸于點A（0，-1），拋物線最高點的縱坐標為$\frac{13}{3}$．
（1）求拋物線的解析式；
（2）點B在第一象限內的拋物線上，其橫坐標為t（t≤4），BC⊥x軸于點C，點D在線段OC的延長線上，BD=AD，當CD=1時，求t的值；
（3）在（2）的條件下，點E在第一象限對稱軸右側的拋物線上，直線CE交y軸于點F，直線DE交y軸于點G，當EC•ED=CF•DG時，求點E的坐標．

Answer 1

分析 （1）將x=0代入可求得b的值，然后依據配方法將函數關系式變形為y=a（x-4）²-16a-1，最后依據頂點縱坐標為$\frac{13}{3}$可求得a的值，從而可求得拋物線的解析式；
（2）先根據題意畫出圖形，設點B的坐標為（t，-$\frac{1}{3}$t²+$\frac{8}{3}$t-1），則點D（t+1，0）．然后依據HL可證明Rt△OAD≌Rt△CDB，從而得到OD=BC，然后由OD=BC列出關于t的方程，于是可求得t的值；
（3）過點G作GM∥x軸，過點E作EM∥y軸，過點C作CH∥y軸，過點D作DI∥y軸．依據平行線分線段成立比例定理可得到：MH：GH=GI：IM．設點E的橫坐標為x．然后依據C、D兩點的坐標可求得GH、GI、HM、IM的長，然后依據比例關系列方程求解即可．

解答 解：（1）∵將x=0代入得：b=-1，
∴拋物線的解析式為y=ax²-8ax-1．
∴y=a（x²-8x+16-16）-1=a（x-4）²-16a-1．
∵拋物線最高點的縱坐標為$\frac{13}{3}$，
∴-16a-1=$\frac{13}{3}$．
解得：a=-$\frac{1}{3}$．
∴拋物線的解析式為y=-$\frac{1}{3}$x²+$\frac{8}{3}$x-1．
（2）如圖1所示：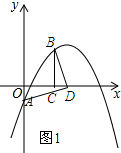

設點B的坐標為（t，-$\frac{1}{3}$t²+$\frac{8}{3}$t-1），則點D（t+1，0）．
在Rt△OAD和Rt△CDB中$\left\{\begin{array}{l}{OA=CD=1}\\{BD=AD}\end{array}\right.$，
∴Rt△OAD≌Rt△CDB．
∴OD=BC，即t+1=-$\frac{1}{3}$t²+$\frac{8}{3}$t-1，整理得：t²-5t+6=0，解得t=2或t=3．
∴t的值為2或3．
（3）如圖2所示：過點G作GM∥x軸，過點E作EM∥y軸，過點C作CH∥y軸，過點D作DI∥y軸．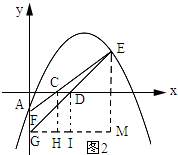

∵EC•ED=CF•DG，
∴CE：FC=DG：ED．
∵AG∥CH∥DI∥EM，
∴EC：CF=MH：GH，DG：ED=GI：IM．
∴MH：GH=GI：IM．
設點E的橫坐標為x．
當C（2，0）、D（3，0）時，則MH=x-2，GH=2，GI=3，MI=x-3．
∵MH：GH=GI：IM，
∴$\frac{x-2}{2}$=$\frac{3}{x-3}$，整理得：x²-5x=0，解得：x=5或x=0（舍去）．
∵將x=5代入拋物線的解析式得y=-$\frac{1}{3}$×25+$\frac{8}{3}$×5-1=4，
∴E（5，4）．
當C（3，0）、D（4，0）時，則MH=x-3，GH=3，GI=4，MI=x-4．
∵MH：GH=GI：IM，
∴$\frac{x-3}{3}$=$\frac{4}{x-4}$，整理得：x²-7x=0，解得：x=7或x=0（舍去）．
∵將x=7代入拋物線的解析式得y=-$\frac{1}{3}$×49+$\frac{8}{3}$×7-1=$\frac{4}{3}$，
∴E（7，$\frac{4}{3}$）．
綜上述所，點E的坐標為（5，4）或（7，$\frac{4}{3}$）．

點評 本題主要考查的是二次函數的綜合應用，解答本題主要應用了待定系數法求二次函數的解析式、全等三角形的性質和判定、平行線分線段成比例定理的應用，依據平行線分線段成比例得到MH：GH=GI：IM是解題的關鍵．