
【題目】綜合與探究
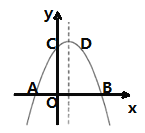
如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,頂點坐標為點
,頂點坐標為點![]() .
.
(1)求此拋物線的解析式;
(2)點![]() 為拋物線對稱軸上一點,當
為拋物線對稱軸上一點,當![]() 最小時,求點
最小時,求點![]() 坐標;
坐標;
(3)在第一象限的拋物線上有一點![]() ,當
,當![]() 面積最大時,求點
面積最大時,求點![]() 坐標;
坐標;
(4)在![]() 軸下方拋物線上有一點
軸下方拋物線上有一點![]() ,
,![]() 面積為6,請直接寫出點
面積為6,請直接寫出點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)點
;(2)點![]() 坐標為
坐標為![]() ;(3)點
;(3)點![]() 坐標為
坐標為![]() ;(4)
;(4)![]() 、
、![]() .
.
【解析】
(1)設拋物線解析式為![]() ,將點B的坐標代入,即可求解;
,將點B的坐標代入,即可求解;
(2)點A關于函數對稱軸的對稱點為B,連接BC交函數對稱軸于點P,此時點P即為所求點,即可求解;
(3)利用![]() ,結合二次函數的最值問題,即可求解;
,結合二次函數的最值問題,即可求解;
(4)利用三角形面積公式可求得點H的縱坐標,即可求解.
(1) ∵拋物線的頂點坐標為點![]() (
(![]() )
)
設拋物線解析式為![]() ,
,
將點![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,
∴解析式為:![]() ;
;
(2) 函數的表達式為:![]() ,
,
令![]() ,則
,則![]() ,
,
解得:![]() 或
或![]() ,
,
令![]() ,則
,則![]() ,
,
故點A、C的坐標分別為(-1,0)、(0,2),
點A關于函數對稱軸的對稱點為B,連接BC交函數對稱軸于點P,此時點P即為所求點,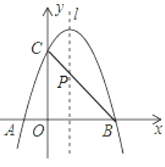
設直線BC的表達式為:![]() ,
,
將點B、C的坐標代入一次函數表達式:![]() 得:
得:
![]() ,
,
解得:![]() ,
,
故直線BC的表達式為:![]() ,
,
當![]() 時,
時,![]() ,
,
故點![]() 的坐標為
的坐標為![]() ;
;
(3)過點M作MH∥y軸交AB于點H,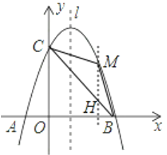
設點![]() ,則點
,則點![]() ,
,![]()
![]()
![]()
![]()
∴當![]() 時,
時,![]() 最大,
最大,
將![]() 代入
代入![]() 得:
得:![]() ,
,
此時,點M的坐標為:![]() ;
;
(4)設點H的縱坐標為y,
![]() ,
,
解得:![]() ,
,
∵點![]() 軸下方,
軸下方,
∴![]() ,
,
將![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴點![]() 的坐標為:
的坐標為:![]() ,
,![]()


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
【題目】在矩形ABCD中作圖:①分別以點B,C為圓心,BC長為半徑畫弧,分別交AD于點H,G;②分別以點B,C為圓心,大于BC的一半長為半徑畫弧,兩弧相交于點E,F;③作直線EF,交AD于點P.下列結論不一定成立的是( )
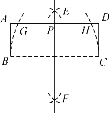
A.BC=BHB.CG=AD
C.PB=PCD.GH=2AB
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與反比例函數
與反比例函數![]() 的圖象相交于
的圖象相交于![]() 、
、![]() 兩點,過
兩點,過![]() 、
、![]() 兩點分別作
兩點分別作![]() 軸的垂線,垂足分別為點
軸的垂線,垂足分別為點![]() 、
、![]() ,連接
,連接![]() 、
、![]() ,則四邊形
,則四邊形![]() 的面積為( )
的面積為( )
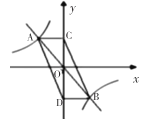
A.4B.8C.12D.24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-2(k-3)x+k2-4k-1=0.
(1)若這個方程有實數根,求k的取值范圍;
(2)若這個方程有一個根為1,求k的值;
查看答案和解析>>
科目:初中數學 來源: 題型:
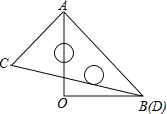
【題目】一副三角板按如圖所示疊放在一起,若固定△AOB,將△ACD繞著公共頂點A,按順時針方向旋轉α度(0°<α<180°),當△ACD的一邊與△AOB的某一邊平行時,相應的旋轉角α的值是___.
查看答案和解析>>
科目:初中數學 來源: 題型:
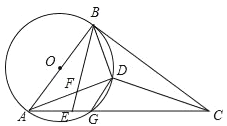
【題目】如圖:AB是⊙O的直徑,AC交⊙O于G,E是AG上一點,D為△BCE內心,BE交AD于F,且∠DBE=∠BAD.
(1)求證:BC是⊙O的切線;
(2)求證:DF=DG;
(3)若∠ADG=45°,DF=1,則有兩個結論:①ADBD的值不變;②AD-BD的值不變,其中有且只有一個結論正確,請選擇正確的結論,證明并求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解班級學生數學課前預習的具體情況,鄭老師對本班部分學生進行了為期一個月的跟蹤調查,他將調查結果分為四類:A:很好;B:較好;C:一般;D:不達標,并將調查結果繪制成以下兩幅不完整的統計圖,請你根據統計圖解答下列問題:

(1)C類女生有 名,D類男生有 名,將上面條形統計圖補充完整;
(2)扇形統計圖中“課前預習不達標”對應的圓心角度數是 ;
(3)為了共同進步,鄭老師想從被調查的A類和D類學生中各隨機機抽取一位同學進行“一幫一”互助學習,請用畫樹狀圖或列表的方法求出所選兩位同學恰好是一男一女同學的概率,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,BE平分∠ABC交AC于點E,過點E作ED∥BC交AB于點D.
(1)求證:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的長.
=2,DE=6,求BC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com