三項式x2-x-2n能分解為兩個整系數一次因式的乘積
(1)若1≤n≤30,且n是整數,則這樣的n有多少個?
(2)當n≤2005時,求最大整數n
【答案】
分析:(1)利用公式法求出x
2-x-2n=0的根,將n從1至30代入開平方驗證,舍去不合題意得,得到最終n的取值及個數.
(2)觀察數列1,3,6,10,15,21,28,尋找規律,將基本規律的代數式代入求值.
解答:解:
(1)x
2-x-2n=
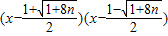
(3分)
則應有1+8n=9,25,49,81,121,169,225,289(7分)
相應解得n=1,3,6,10,15,21,28,36(舍去)
故當1≤n≤30時,滿足條件的整數n有7個(10分)
(2)觀察數列1,3,6,10,發現
1=1,3=1+2,6=1+2+3,10=1+2+3+4
故n=1+2+3+…+k≤2005
∴
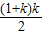
≤2005
驗證得當k=62時,n取最大值為1953(20分)
點評:本題考查因式分解的應用.解決(1)主要是通過公式法分解出因式,再將符合條件的n代入逐個驗證;(2)關鍵是觀察數列找到規律.

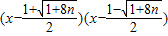 (3分)
(3分)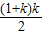 ≤2005
≤2005
