
【題目】如圖1,平面內有一點P到△ABC的三個頂點的距離分別為PA、PB、PC,若有PA2+PB2=PC2,則稱點P為△ABC關于點C的勾股點.

(1)如圖2,在4×3的方格紙中,每個小正方形的邊長均為1,△ABC的頂點在格點上,請找出所有的格點P,使點P為△ABC關于點A的勾股點.
(2)如圖3,△ABC為等腰直角三角形,P是斜邊BC延長線上一點,連接AP,以AP為直角邊作等腰直角三角形APD(點A、P、D順時針排列)∠PAD=90°,連接DC,DB,求證:點P為△BDC關于點D的勾股點.
(3)如圖4,點E是矩形ABCD外一點,且點C是△ABE關于點A的勾股點,若AD=8,CE=5,AD=DE,求AE的長.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)如圖2-1,圖2-2,求出PA2,PB2,PC2,得到PC2+PB2=PA2,即得出點P是△ABC關于點A的勾股點;
(2)證明△ABD≌△ACP(SAS),得出BD=CP,∠ABD=∠ACP=135°,證明∠DBP=90°,則結論得證;
(3)由條件“點C是△ABE關于點A的勾股點”可得CE=CD=5,如圖3,過點E作MN⊥AB于點M,交DC的延長線于點N,設AM=DN=x,則CN=DN﹣CD=x﹣5,由勾股定理可得82﹣x2=52﹣(x﹣5)2,求出x的值,進而求出AM,ME的長,則答案可得出.
解:(1)如圖2-1,
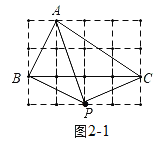
∵PA2=12+32=10,PB2=12+22=5,PC2=PB2=5,
∴PA2=PC2+PB2,
∴點P是△ABC關于點A的勾股點;
如圖2-2,
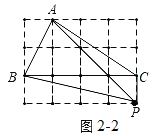
∵PA2=32+32=18,PB2=12+42=17,PC2=1,
∴PA2=PC2+PB2,
∴點P是△ABC關于點A的勾股點;
(2)∵△ABC和△APD為等腰直角三角形,
∴AB=AC,AD=AP,∠BAC=∠DAP=90°,
∴∠BAC﹣∠DAC=∠DAP﹣∠DAC,
即∠BAD=∠CAP,
∴△ABD≌△ACP(SAS),
∴BD=PC,∠ABD=∠ACP=135°,
∵∠ABC=45°,
∴∠DBP=∠ABD﹣∠ABC=135°﹣45°=90°,
∴BD2+PB2=PD2,
∴PC2+PB2=PD2,
∴點P為△BDC關于點D的勾股點.
(3)解:∵矩形ABCD中,AD=8,
∴AD=BC=8,CD=AB,
∵AD=DE,
∴DE=8,
∵點C是△ABE關于點A的勾股點,
∴AC2=CB2+CE2,
∵AC2=AB2+BC2,
∴CE=CD=5,
如圖3,過點E作MN⊥AB于點M,交DC的延長線于點N,
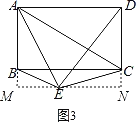
∴∠AME=∠MND=90°,
∴四邊形AMND是矩形,
∴MN=AD=8,AM=DN,
設AM=DN=x,則CN=DN﹣CD=x﹣5,
∵Rt△DEN中,EN2+DN2=DE2;Rt△CEN中,EN2+CN2=CE2,
∴DE2﹣DN2=CE2﹣CN2,
∴82﹣x2=52﹣(x﹣5)2
解得:x=![]() ,
,
∴EN═![]() =
=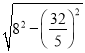 =
=![]() ,AM=DN=
,AM=DN=![]() ,
,
∴ME=MN﹣EN=8﹣![]() =
=![]() ,
,
∴Rt△AME中,AE=![]() =
=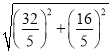 =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c的圖象如圖所示,下列說法正確的是( )
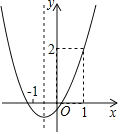
A.abc>0B.a﹣b+c=2
C.4ac﹣b2<0D.當x>﹣1時,y隨x增大而增大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個矩形紙片![]() 放置在平面直角坐標系中,點
放置在平面直角坐標系中,點![]() 點
點![]() 點
點![]()
![]() 是邊
是邊![]() 上的一點(點
上的一點(點![]() 不與點
不與點![]() 重合),沿著
重合),沿著![]() 折疊該紙片,得點
折疊該紙片,得點![]() 的對應點
的對應點![]() .
.
(1)如圖①,當點![]() 落在邊
落在邊![]() 上時,求點
上時,求點![]() 的坐標;
的坐標;

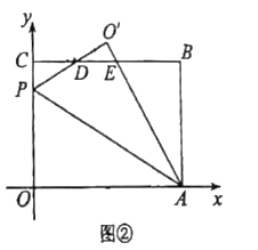
(2)若點![]() 落在邊
落在邊![]() 的上方,
的上方,![]() 與分別與邊
與分別與邊![]() 交于點
交于點![]() .
.
①如圖②,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
②當![]() 時,求點
時,求點![]() 的坐標(直接寫出結果即可).
的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
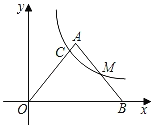
【題目】如圖,在平面直角坐標系中,△OAB的邊OB在x軸的正半軸上,AO=AB,M是邊AB的中點,經過點M的反比例函數y=![]() (k>0,x>0)的圖象與邊OA交于點C,則
(k>0,x>0)的圖象與邊OA交于點C,則![]() 的值為__.
的值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
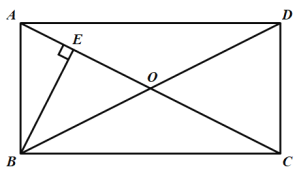
【題目】如圖,在![]() ABCD中,對角線AC,BD交于點O,OA=OB,過點B作BE⊥AC于點E.
ABCD中,對角線AC,BD交于點O,OA=OB,過點B作BE⊥AC于點E.
(1)求證:![]() ABCD是矩形;
ABCD是矩形;
(2)若AD=![]() ,cos∠ABE=
,cos∠ABE=![]() ,求AC的長.
,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
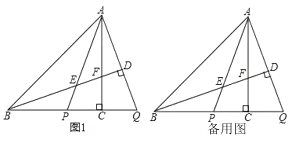
【題目】如圖,在等腰直角△ABC中,∠ACB=90點P在線段BC上,延長BC至點Q,使得CQ=CP,連接AP,AQ.過點B作BD⊥AQ于點D,交AP于點E,交AC于點F.K是線段AD上的一個動點(與點A,D不重合),過點K作GN⊥AP于點H,交AB于點G,交AC于點M,交FD的延長線于點N.
(1)依題意補全圖1;
(2)求證:NM=NF;
(3)若AM=CP,用等式表示線段AE,GN與BN之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
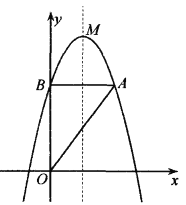
【題目】如圖,拋物線![]() 交
交![]() 軸于點
軸于點![]() 頂點為
頂點為![]() 軸,交拋物線于點
軸,交拋物線于點![]() 已知該拋物線的對稱軸為直線
已知該拋物線的對稱軸為直線![]() .
.
(1)求![]() 的值和點
的值和點![]() 的坐標.
的坐標.
(2)將拋物線向下平移![]() 個單位,使平移后得到的拋物線頂點落在
個單位,使平移后得到的拋物線頂點落在![]() 的內部(不包括
的內部(不包括![]() 的邊界),則
的邊界),則![]() 的取值范圍為 .
的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》中記載:“今有上禾三秉,益實六斗,當下禾十秉.下禾五秉,益實一斗,當上禾二秉.問上、下禾實一秉各幾何?”其大意是:今有上等稻子三捆,若打出來的谷子再加六斗,則相當于十捆下等稻子打出來的谷子.有下等稻子五捆,若打出來的谷子再加一斗,則相當于兩捆上等稻子打岀來的谷子.問上等、下等稻子每捆能打多少斗谷子?設上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根據題意,可列方程組為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com