
【題目】參照學習函數的過程與方法,探究函數![]()
![]() 的圖象與性質列表:
的圖象與性質列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描點:在平面直角坐標系中,以自變量x的取值為橫坐標,以![]() 相應的函數值為縱坐標,描出相應的點,如圖所示:
相應的函數值為縱坐標,描出相應的點,如圖所示:
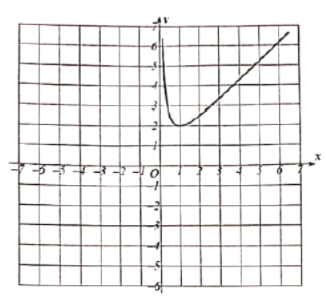
(1)請補全函數圖象:
(2)觀察圖象并分析表格,回答下列問題:
①當![]() 時,y隨x的增大而_________;(填“增大”或“減小”)
時,y隨x的增大而_________;(填“增大”或“減小”)
②圖象關于點__________中心對稱.(填點的坐標)
③當![]() 時,
時,![]() 的最小值是_________.
的最小值是_________.
(3)結合函數圖象,當![]() 時,求x的取值范圍.
時,求x的取值范圍.
 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】如圖,等腰三角形 ABC 中,AC=BC=13,AB=10.以 BC 為直徑作⊙O 交 AB 于點 D,交 AC 于點 G,DF⊥AC,垂足為 F,交 CB 的延長線于點 E.
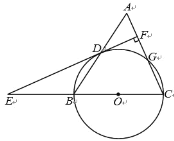
(1)求證:直線 EF 是⊙O 的切線;
(2)求 sin∠E 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線,![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且拋物線
,且拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() .
.
(1)拋物線的表達式;
(2)若拋物線![]() 與拋物線
與拋物線![]() 關于直線
關于直線![]() 對稱,拋物線
對稱,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),要使
左側),要使![]() ,求所有滿足條件的拋物線
,求所有滿足條件的拋物線![]() 的表達式.
的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個矩形紙片OABC放置在平面直角坐標系xOy內,點A(6,0),點C(0,4),點O(0,0).點P是線段BC上的動點,將△OCP沿OP翻折得到△OC′P.

(Ⅰ)如圖①,當點C′落在線段AP上時,求點P的坐標;
(Ⅱ)如圖②,當點P為線段BC中點時,求線段BC′的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一條筆直的公路上順次有![]() 、
、![]() 、
、![]() 三地,甲車從
三地,甲車從![]() 地出發往
地出發往![]() 地勻速行駛,到達
地勻速行駛,到達![]() 地后停止,在甲車出發的同時,乙車從
地后停止,在甲車出發的同時,乙車從![]() 地出發往
地出發往![]() 地勻速行駛,到達
地勻速行駛,到達![]() 地停留
地停留![]() 小時后,調頭按原速向
小時后,調頭按原速向![]() 地行駛,若
地行駛,若![]() 兩地相距
兩地相距![]() 千米,在兩車行駛的過程中,甲、乙兩車之間的距離(千米)與乙車行駛時間
千米,在兩車行駛的過程中,甲、乙兩車之間的距離(千米)與乙車行駛時間![]() (小時)之間的函數圖象如圖所示,則在他們出發后經過_________小時相遇.
(小時)之間的函數圖象如圖所示,則在他們出發后經過_________小時相遇.
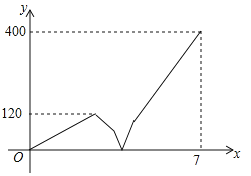
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為測量大樓![]() 的高度,從距離大樓底部
的高度,從距離大樓底部![]() 30米處的
30米處的![]() ,有一條陡坡公路,車輛從
,有一條陡坡公路,車輛從![]() 沿坡度
沿坡度![]() ,坡面長13米的斜坡到達
,坡面長13米的斜坡到達![]() 后,觀測到大樓的頂端
后,觀測到大樓的頂端![]() 的仰角為30°,則大樓的高度為( )米.
的仰角為30°,則大樓的高度為( )米.
(精確到0.1米,![]() ,
,![]() )
)
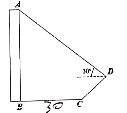
A.26.0B.29.2C.31.1D.32.2
查看答案和解析>>
科目:初中數學 來源: 題型:
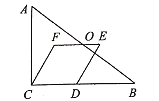
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 為射線
為射線![]() 上的動點,以
上的動點,以![]() 為邊,在
為邊,在![]() 的同側作菱形
的同側作菱形![]() ,使得
,使得![]() .若菱形
.若菱形![]() 的邊
的邊![]() 經過線段
經過線段![]() 的中點
的中點![]() .
.
(1)將菱形![]() 沿射線
沿射線![]() 向右平移,記平移中的菱形
向右平移,記平移中的菱形![]() 菱形
菱形![]() ,當點
,當點![]() 與點
與點![]() 重合時停止平移.設平移的距離為
重合時停止平移.設平移的距離為![]() ,是否存在這樣的
,是否存在這樣的![]() ,使△BDE是等腰三角形?若存在,求出
,使△BDE是等腰三角形?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(2)在(1)問的平移過程中,設菱形![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() ,請直接寫出
,請直接寫出![]() 與
與![]() 之間的函數關系式以及自變量
之間的函數關系式以及自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
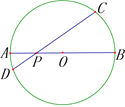
【題目】已知:AB是⊙O的直徑,P是OA上一點,過點P作⊙O的非直徑的弦CD.
(1)若PA=2,PB=10,∠CPB=30°,求CD長;
(2)求證:PCPD=PAPB;
(3)設⊙O的直徑為8,若PC、PD是方程![]() ,求m的范圍.
,求m的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com