
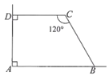
【題目】如圖,利用一個直角墻角修建一個梯形儲料場ABCD,其中∠C=120°.若新建墻BC與CD總長為12m,則該梯形儲料場ABCD的最大面積是( )
A.18m2B.![]() m2C.
m2C.![]() m2D.
m2D.![]() m2
m2
【答案】C
【解析】
過點C作CE⊥AB于E,則四邊形ADCE為矩形,CD=AE=x,∠DCE=∠CEB=90°,則
∠BCE=∠BCD-∠DCE=30°,BC=12-x,由直角三角形的,性質(zhì)得出![]() 得出
得出![]() ,又梯形面積公式求出梯形ABCD的面積S與x之間的函數(shù)關(guān)系式,根據(jù)二次函數(shù)的性質(zhì)求解.
,又梯形面積公式求出梯形ABCD的面積S與x之間的函數(shù)關(guān)系式,根據(jù)二次函數(shù)的性質(zhì)求解.
解:如圖,過點C作CE⊥AB于E,
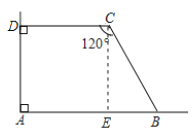
則四邊形ADCE為矩形,CD=AE=x,∠DCE=∠CEB=90°,則∠BCE=∠BCD-∠DCE=30°,BC=12-x,
在Rt△CBE中,∵∠CEB=90°,
![]()
![]()
∴梯形ABCD面積
![]()
∴當(dāng)x=4時,S最大=24![]() .
.
即CD長為4 m時,使梯形儲料場ABCD的面積最大為24 ![]() m2;
m2;
故選:C.


 字詞句篇與同步作文達(dá)標(biāo)系列答案
字詞句篇與同步作文達(dá)標(biāo)系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,
,![]() 是邊
是邊![]() 上一點,
上一點,![]() ,將
,將![]() ,
,![]() 分別沿折痕
分別沿折痕![]() ,
,![]() 向內(nèi)折疊,點
向內(nèi)折疊,點![]() ,
,![]() 在點
在點![]() 處重合,過點
處重合,過點![]() 作
作![]() ,交
,交![]() 的延長線于
的延長線于![]() .則下列結(jié)論正確的有( )
.則下列結(jié)論正確的有( )
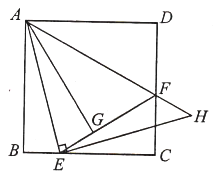
①![]() ;②
;②![]() 為等腰直角三角形;③點
為等腰直角三角形;③點![]() 是
是![]() 的中點;④
的中點;④![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與y軸交于點C,與x軸交于A,B兩點,其中點B的坐標(biāo)為B(4,0),拋物線的對稱軸交x軸于點D,CE∥AB,并與拋物線的對稱軸交于點E現(xiàn)有下列結(jié)論:①b2﹣4a<0;②b>0;③5a+b<0;④AD+CE=4.其中正確結(jié)論個數(shù)為( )
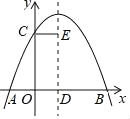
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,A、B為x軸上兩點,C、D為y軸上的兩點,經(jīng)
中,A、B為x軸上兩點,C、D為y軸上的兩點,經(jīng)
過點A、C、B的拋物線的一部分C1與經(jīng)過點A、D、B的拋物線的一部分C2組合成一條封閉曲線,我們把這條封
閉曲線稱為“蛋線”.已知點C的坐標(biāo)為(0,![]() ),點M是拋物線C2:
),點M是拋物線C2:![]() (
(![]() <0)的頂點.
<0)的頂點.
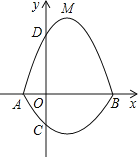
(1)求A、B兩點的坐標(biāo);
(2)“蛋線”在第四象限上是否存在一點P,使得△PBC的面積最大?若存在,求出△PBC面積的最大值;若不存在,請說明理由;
(3)當(dāng)△BDM為直角三角形時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,將正方形![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 后得到正方形
后得到正方形![]() ,依此方式,繞點
,依此方式,繞點![]() 連續(xù)旋轉(zhuǎn)2019次得到正方形
連續(xù)旋轉(zhuǎn)2019次得到正方形![]() ,如果點
,如果點![]() 的坐標(biāo)為(1,0),那么點
的坐標(biāo)為(1,0),那么點![]() 的坐標(biāo)為________.
的坐標(biāo)為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)解方程:![]()
(2)如圖,正方形網(wǎng)格中,每個小正方形的邊長都是一個單位長度,在平面直角坐標(biāo)系內(nèi),![]() 的三個頂點坐標(biāo)分別為
的三個頂點坐標(biāo)分別為![]() ,
,![]() ,
,![]() .
.
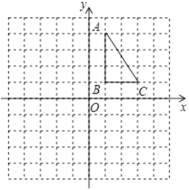
①畫出![]() 關(guān)于
關(guān)于![]() 軸對稱的
軸對稱的![]() ;
;
②畫出![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 后的
后的![]() ;
;
③在②的條件下,求線段![]() 掃過的面積(結(jié)果保留
掃過的面積(結(jié)果保留![]() ).
).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】 如圖,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,拋物線
,拋物線![]() 經(jīng)過點
經(jīng)過點![]() ,交
,交![]() 軸于點
軸于點![]() .點
.點![]() 為拋物線上一動點,過點
為拋物線上一動點,過點![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
于點![]() ,設(shè)點
,設(shè)點![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
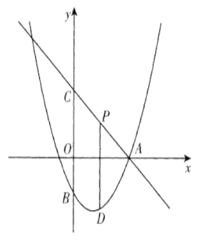
(1)求拋物線的解析式;
(2)當(dāng)點![]() 在直線
在直線![]() 下方的拋物線上運動時,求線段
下方的拋物線上運動時,求線段![]() 長度的最大值;
長度的最大值;
(3)若點![]() 是平面內(nèi)任意一點,是否存在點
是平面內(nèi)任意一點,是否存在點![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形?若存在,請直接出
為頂點的四邊形為菱形?若存在,請直接出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)課外興趣活動小組準(zhǔn)備圍建一個矩形花草園,其中一邊靠墻,另外三邊周長為30米的籬笆圍成.已知墻長為16米(如圖所示),設(shè)這個花草園垂直于墻的一邊長為x米.
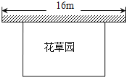
(1)若花草園的面積為100平方米,求x;
(2)若平行于墻的一邊長不小于10米,這個花草園的面積有最大值和最小值嗎?如果有,求出最大值和最小值;如果沒有,請說明理由;
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com