解:(1)△ABC是等腰三角形.
∵BD=BC=AD,BD平分∠ABC,
∴∠C=∠BDC,∠A=∠ABD=∠CBD.
設∠A=x,則∠C=∠BDC=2x,∠ABC=2x.
∴∠C=∠ABC,
∴AB=AC,即△ABC是等腰三角形.
(2)在△ABC中,∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得 x=36°.
∴∠A=36°,∠C=72°,∠ABC=72°.
分析:根據已知條件,圖中△BCD、△ABD是等腰三角形.根據“等邊對等角”和三角形內角和定理可分別求出△ABC各角的度數,并判斷形狀.
點評:此題考查等腰三角形的性質與判定及三角形內角和定理,理順角之間的關系是關鍵.

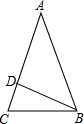 如圖,BD是△ABC的角平分線,且BD=BC=AD.
如圖,BD是△ABC的角平分線,且BD=BC=AD.
