
 如圖,C在以AB為直徑的半圓⊙O上,I是△ABC的內心,AI,BI 的延長線分別交半圓⊙O于點D,E,AB=6,則DE的長為( )
如圖,C在以AB為直徑的半圓⊙O上,I是△ABC的內心,AI,BI 的延長線分別交半圓⊙O于點D,E,AB=6,則DE的長為( )| A. | 3 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 5 |
分析 連結OD、OE.根據三角形內心的性質得出∠CAB=2∠DAB,∠ABC=2∠ABE.由圓周角定理得出∠C=90°,∠DOB=2∠DAB,∠AOE=2∠ABE,進而得出∠DOB+∠AOE=90°,利用平角的定義得出∠DOE=90°,又OD=OE=$\frac{1}{2}$AB=3,然后根據勾股定理即可求出DE.
解答 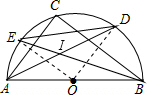 解:如圖,連結OD、OE.
解:如圖,連結OD、OE.
∵I是△ABC的內心,
∴∠CAB=2∠DAB,∠ABC=2∠ABE.
∵C在以AB為直徑的半圓⊙O上,
∴∠C=90°,
∴∠CAB+∠ABC=90°,
∴2∠DAB+2∠ABE=90°,
∵∠DOB=2∠DAB,∠AOE=2∠ABE,
∴∠DOB+∠AOE=90°,
∴∠DOE=180°-(∠DOB+∠AOE)=90°,
∵OD=OE=$\frac{1}{2}$AB=3,
∴DE=$\sqrt{O{D}^{2}+O{E}^{2}}$=3$\sqrt{2}$.
故選B.
點評 本題考查了三角形的內切圓與內心:與三角形各邊都相切的圓叫三角形的內切圓,三角形的內切圓的圓心叫做三角形的內心,這個三角形叫做圓的外切三角形.三角形的內心就是三角形三個內角角平分線的交點.也考查了圓周角定理,平角的定義以及勾股定理.作出輔助線證明∠DOE=90°是解題的關鍵.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,等腰Rt△ABC的直角頂點在y軸上,斜邊BC在x軸上,AB=AC=4$\sqrt{2}$,D為斜邊BC的中點,點P由點A出發沿線段AB做勻速運動,P′是點P關于AD的對稱點,P′P交y軸于點F,點Q由點D出發沿射線DC方向做勻速運動,且滿足四邊形QDPP′是平行四邊形,設?QDPP′的面積為S,DQ=x.
如圖,在平面直角坐標系中,等腰Rt△ABC的直角頂點在y軸上,斜邊BC在x軸上,AB=AC=4$\sqrt{2}$,D為斜邊BC的中點,點P由點A出發沿線段AB做勻速運動,P′是點P關于AD的對稱點,P′P交y軸于點F,點Q由點D出發沿射線DC方向做勻速運動,且滿足四邊形QDPP′是平行四邊形,設?QDPP′的面積為S,DQ=x.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
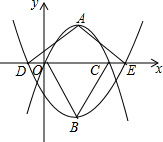 如圖,在平面直角坐標系中,拋物線y=a1(x-2)2+2與y=a2(x-2)2-3的頂點分別為A,B,與x軸分別交于點O,C,D,E.若點D的坐標為(-1,0),則△ADE與△BOC的面積比為1.
如圖,在平面直角坐標系中,拋物線y=a1(x-2)2+2與y=a2(x-2)2-3的頂點分別為A,B,與x軸分別交于點O,C,D,E.若點D的坐標為(-1,0),則△ADE與△BOC的面積比為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
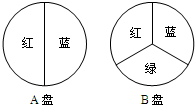 用如圖所示的A,B兩個轉盤進行“配紫色”游戲(紅色和藍色在一起配成了紫色).小亮和小剛同時轉動兩個轉盤,若配成紫色,小亮獲勝,否則小剛獲勝.這個游戲對雙方公平嗎?請你并說明理由.
用如圖所示的A,B兩個轉盤進行“配紫色”游戲(紅色和藍色在一起配成了紫色).小亮和小剛同時轉動兩個轉盤,若配成紫色,小亮獲勝,否則小剛獲勝.這個游戲對雙方公平嗎?請你并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
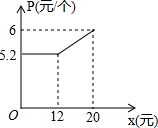 某企業接到一批零件的加工任務,要求在20天內完成,這批零件的出廠價為每個6元.為按時完成任務,該企業招收了新工人,在6天的培訓期內,新工人小亮第x天能加工80x個零件,培訓后小亮第x天內加工的零件個數為(50x+200)個.
某企業接到一批零件的加工任務,要求在20天內完成,這批零件的出廠價為每個6元.為按時完成任務,該企業招收了新工人,在6天的培訓期內,新工人小亮第x天能加工80x個零件,培訓后小亮第x天內加工的零件個數為(50x+200)個.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
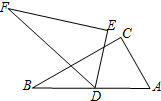 兩個完全重合的直角三角形Rt△ABC與Rt△DEF兩直角邊分別為3cm、4cm,點D放置在AB的中點,△DEF可以繞點D轉動,當Rt△DEF旋轉到一邊與AB垂直時,兩三角形重疊部分面積為$\frac{75}{64}$、$\frac{69}{32}$、$\frac{25}{12}$.
兩個完全重合的直角三角形Rt△ABC與Rt△DEF兩直角邊分別為3cm、4cm,點D放置在AB的中點,△DEF可以繞點D轉動,當Rt△DEF旋轉到一邊與AB垂直時,兩三角形重疊部分面積為$\frac{75}{64}$、$\frac{69}{32}$、$\frac{25}{12}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com