【題目】我市某中學決定在學生中開展丟沙包、打籃球、跳大繩和踢毽球四種項目的活動，為了解學生對四種項目的喜歡情況，隨機調查了該校m名學生最喜歡的一種項目（每名學生必選且只能選擇四種活動項目的一種），并將調查結果繪制成如下的不完整的統計圖表：
學生最喜歡的活動項目的人數統計表
項目 | 學生數（名） | 百分比 |
丟沙包 | 20 | 10% |
打籃球 | 60 | p% |
跳大繩 | n | 40% |
踢毽球 | 40 | 20% |
根據圖表中提供的信息，解答下列問題：
（1）m= ， n= ， p=；
（2）請根據以上信息直接補全條形統計圖；
（3）根據抽樣調查結果，請你估計該校2000名學生中有多少名學生最喜歡跳大繩．
科目：初中數學 來源： 題型：
【題目】如圖是一張平行四邊形紙片ABCD，要求利用所學知識將它變成一個菱形，甲、乙兩位同學的作法分別如下：
對于甲、乙兩人的作法，可判斷( )
A. 甲正確，乙錯誤 B. 甲錯誤，乙正確
C. 甲、乙均正確 D. 甲、乙均錯誤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某居民小區為了綠化小區環境，建設和諧家園，準備將一塊周長為76米的長方形空地，設計成長和寬分別相等的9塊小長方形，如圖所示，計劃在空地上種上各種花卉，經市場預測，綠化每平方米空地造價210元，請計算，要完成這塊綠化工程，預計花費多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探索：小明在研究數學問題：已知AB∥CD，AB和CD都不經過點P，探索∠P與∠C的數量關系．
發現：在如圖中，：∠APC=∠A+∠C；如圖
小明是這樣證明的：過點P作PQ∥AB
∴∠APQ=∠A(_ __)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(__ _)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
(1)為小明的證明填上推理的依據；
(2)應用：①在如圖中，∠P與∠A、∠C的數量關系為__ _；
②在如圖中,若∠A=30
，∠C=70 ，則∠P的度數為__ _；
(3)拓展：在如圖中，探究∠P與∠A,∠C的數量關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
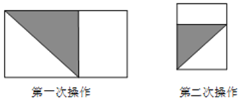
【題目】將長為1，寬為
的長方形紙片
如圖那樣折一下，剪下一個邊長等于長方形的寬度的正方形
稱為第一次操作
；再把剩下的長方形如圖那樣折一下，剪下一個邊長等于此時長方形寬度的正方形稱為第二次操作；如些反復操作下去，若在第
次操作后剩下的長方形為正方形，則操作終止．
第一次操作后，剩下的長方形兩邊長分別為______和 ；用含的代數式表示
若第二次操作后，剩下的長方形恰好是正方形，則求的值，寫出解答過程；
若第三次操作后，剩下的長方形恰好是正方形，畫出圖形，試求的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用若干塊如左圖所示的正方形或長方形紙片拼成圖（1）和圖（2）
（1）如圖（1），若AD=7，AB=8，求
與
的值；
（2）如圖（1），若長方形ABCD的面積為35，其中陰影部分的面積為20，求長方形ABCD的周長；
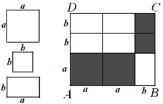
圖（1）
（3）如圖（2），若AD的長度為5，AB的長度為
．
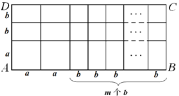
圖（2）
①當
=________，=_________時，，的值有無數組；
②當________，_________時，，的值不存在．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把一矩形紙片OABC放入平面直角坐標系xoy中，使OA，OC分別落在x軸、y軸上，現將紙片OABC沿OB折疊，折疊后點A落在點A'的位置，若OA=1，OB=2，則點A'的坐標為（ ）
A.
B.
C.（ 
）
D.（ 
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知在平面直角坐標系中，過點
向x軸作垂線，垂足為點M，點F從點M出發，沿x軸正方向以每秒1個單位長度的速度運動，連接AF，過點A作
交y軸于點E，設點F運動的時間是t秒
．
若點E在y軸的負半軸上
如圖所示
，求證：
；
如果點F運動時間是4秒．
求直線AE的表達式；
若直線AE與x軸的交點為B，C是y軸上一點，使
，求出C的坐標；
在點F運動過程中，設
，
，試用含m的代數式表示n．
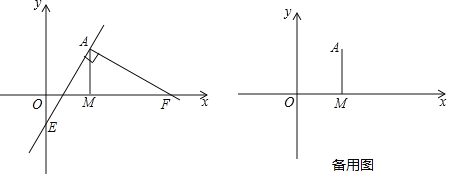
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
