
 如圖,在四邊形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四邊形ABCD的面積.
如圖,在四邊形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四邊形ABCD的面積. 分析 連接AC,在Rt△ABC中根據勾股定理求出AC的長,再由勾股定理的逆定理判斷出△ADC是直角三角形,根據S四邊形ABCD=S△ABC+S△ACD即可得出結論.
解答 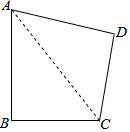 解:連接AC,在Rt△ABC中,
解:連接AC,在Rt△ABC中,
∵AB=8,BC=6,∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10.
在△ADC中,∵AD=CD=5$\sqrt{2}$,
∴AD2+CD2=(5$\sqrt{2}$)2+(5$\sqrt{2}$)2=100.
∵AC2=102=100,
∴AD2+CD2=AC2,
∴∠ADC=90°,
∴S四邊形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AD•DC=$\frac{1}{2}$×8×6+$\frac{1}{2}$×5$\sqrt{2}$×5$\sqrt{2}$=24+25=49.
點評 本題考查的是勾股定理及勾股定理的逆定理,不規則幾何圖形的面積,根據題意作出輔助線,構造出直角三角形是解答此題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | x≠3,且x≠-5 | B. | x≠3,且x≠4 | C. | x≠4且 x≠-5 | D. | x≠3,且x≠4且x≠-5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
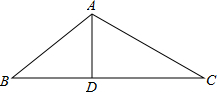 如圖,D為△ABC的BC邊上的一點,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如圖,D為△ABC的BC邊上的一點,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,OP=1,過P作PP1⊥OP,得OP1=$\sqrt{2}$;再過P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法繼續作下去,得OP2016的值等于( )
如圖,OP=1,過P作PP1⊥OP,得OP1=$\sqrt{2}$;再過P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又過P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法繼續作下去,得OP2016的值等于( )| A. | $\sqrt{2014}$ | B. | $\sqrt{2015}$ | C. | $\sqrt{2016}$ | D. | $\sqrt{2017}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
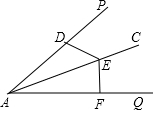 如圖,已知AC平分∠PAQ,D、E、F分別是AP、AC、AQ上的三個動點,下列說法不正確的是( )
如圖,已知AC平分∠PAQ,D、E、F分別是AP、AC、AQ上的三個動點,下列說法不正確的是( )| A. | DE⊥AP,EF⊥AQ,可推出AD=AF | B. | 若DE=EF,可推出AD=AF | ||
| C. | 若∠DEA=∠FEA,可推出AD=AF | D. | 若∠ADE=∠AFE,可推出AD=AF |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
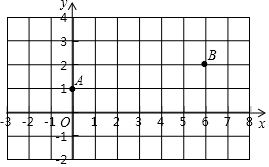 如圖,在平面直角坐標系xOy中,已知點A(0,1),B(6,2),在x軸上找一點P,使得PA+PB最小,則點P的坐標是(4,0),此時△PAB的面積是2.
如圖,在平面直角坐標系xOy中,已知點A(0,1),B(6,2),在x軸上找一點P,使得PA+PB最小,則點P的坐標是(4,0),此時△PAB的面積是2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com