
 如圖一個直角三角形PQR的直角頂點為Q,以其三邊為直徑作三個半圓,矩形STUV的各邊與半圓相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,則STUV的面積是多少平方厘米?
如圖一個直角三角形PQR的直角頂點為Q,以其三邊為直徑作三個半圓,矩形STUV的各邊與半圓相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,則STUV的面積是多少平方厘米?
 QR=
QR= ×8=4,OK=
×8=4,OK= PQ=
PQ= ×6=3厘米,
×6=3厘米, PQ=
PQ= ×6=3,KN=
×6=3,KN= QR=
QR= ×8=4厘米,
×8=4厘米, =10厘米,
=10厘米, ×PR=5厘米,
×PR=5厘米,

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
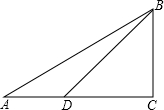 如圖,直角三角形三邊長AB=10cm,AC=ycm,BC=xcm.
如圖,直角三角形三邊長AB=10cm,AC=ycm,BC=xcm.查看答案和解析>>
科目:初中數學 來源: 題型:
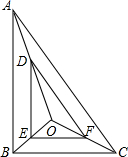 如圖,直角三角形ABC到直角三角形DEF是一個相似變換,AC與DF的長度之比是3:2.
如圖,直角三角形ABC到直角三角形DEF是一個相似變換,AC與DF的長度之比是3:2.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖一個直角三角形PQR的直角頂點為Q,以其三邊為直徑作三個半圓,矩形STUV的各邊與半圓相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,則STUV的面積是多少平方厘米?
如圖一個直角三角形PQR的直角頂點為Q,以其三邊為直徑作三個半圓,矩形STUV的各邊與半圓相切且平行于PQ或者QR.如果PQ=6厘米,QR=8厘米,則STUV的面積是多少平方厘米?查看答案和解析>>
科目:初中數學 來源:2012年上海市蘭生復旦中學理科班教程:勾股定理(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com