
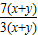 =
= ;
;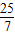 y,
y,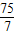 y+3y=
y+3y=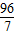 y,4x=
y,4x=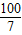 y,4y,滿足題意,
y,4y,滿足題意,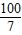 y,
y,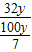 =
=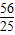 倍;
倍;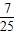 y,
y,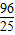 y,4x=
y,4x=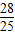 y,4y,滿足題意,
y,4y,滿足題意,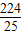 y,斜邊為4y,
y,斜邊為4y,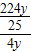 =
=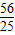 倍,
倍, 或
或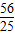 倍.
倍. 或
或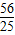 .
.

 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:初中數學 來源: 題型:
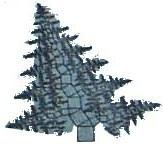 勾股定理揭示了直角三角形三邊之間的關系,其中蘊含著豐富的科學知識和人文價值.如圖所示,是一棵由正方形和含30°角的直角三角形按一定規律長成的勾股樹,樹主干自下而上第一個正方形和第一個直角三角形的面積之和為S1,第二個正方形和第二個直角三角形的面積之和為S2,…,第n個正方形和第n個直角三角形的面積之和為Sn.設第一個正方形的邊長為1.
勾股定理揭示了直角三角形三邊之間的關系,其中蘊含著豐富的科學知識和人文價值.如圖所示,是一棵由正方形和含30°角的直角三角形按一定規律長成的勾股樹,樹主干自下而上第一個正方形和第一個直角三角形的面積之和為S1,第二個正方形和第二個直角三角形的面積之和為S2,…,第n個正方形和第n個直角三角形的面積之和為Sn.設第一個正方形的邊長為1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com