
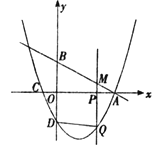
【題目】如圖,在平面直角坐標系中,直線![]() 分別交
分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、
、![]() .點
.點![]() 的坐標是
的坐標是![]() ,拋物線
,拋物線![]() 經過
經過![]() 、
、![]() 兩點且交
兩點且交![]() 軸于點
軸于點![]() .點
.點![]() 為
為![]() 軸上一點,過點
軸上一點,過點![]() 作
作![]() 軸的垂線交直線
軸的垂線交直線![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() ,連結
,連結![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求點![]() 的坐標.
的坐標.
(2)求拋物線的表達式.
(3)當以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形時,求
為頂點的四邊形是平行四邊形時,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)令y=0,代入直線![]() 即可求解;
即可求解;
(2)代入A和C點坐標,聯立方程組即可求解拋物線解析式;
(3)令x=0,代入直線![]() 可求解B點坐標.已知點
可求解B點坐標.已知點![]() 的橫坐標為
的橫坐標為![]() ,則可分別寫出M和Q的含m的坐標,再由平行四邊形的性質可知BD=MQ,據此即可求解.
,則可分別寫出M和Q的含m的坐標,再由平行四邊形的性質可知BD=MQ,據此即可求解.
(1)令y=0,代入直線![]() 可得,x=4,故
可得,x=4,故![]() ;
;
(2)代入A和C點坐標至拋物線解析式,聯立可得:
![]() 解得
解得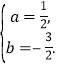
即,![]() .
.
(3)點![]() 的橫坐標為
的橫坐標為![]() ,則可得
,則可得![]() ,
,![]() ,
,
則可得,![]() .
.
令x=0,代入直線![]() 可得y=2,即B(0,2),
可得y=2,即B(0,2),
令x=0,代入拋物線![]() 可得y=-2,即D(0,-2),
可得y=-2,即D(0,-2),
則BD=4,
由平行四邊形的性質可知BD=MQ,則:
![]() ,
,
當![]() 時,解得:
時,解得:![]() (舍),
(舍),![]() ;
;
當![]() =4時,解得:
=4時,解得:![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]() .
.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】在環境創優活動中,某居民小區要在一塊靠墻(墻長25米)的空地上修建一個矩形養雞場,養雞場的一邊靠墻,如果用60m長的籬笆圍成中間有一道籬笆的養雞場,設養雞場平行于墻的一邊BC的長為x(m),養雞場的面積為y(m2)
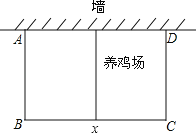
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)養雞場的面積能達到300m2嗎?若能,求出此時x的值,若不能,說明理由;
(3)根據(1)中求得的函數關系式,判斷當x取何值時,養雞場的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
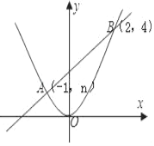
【題目】如圖,一次函數y1=kx+b與二次函數y2=ax2的圖象交于A(﹣1,n),B(2,4)兩點.
(1)利用圖中條件,求兩個函數的解析式;
(2)根據圖象直接寫出使y1<y2的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
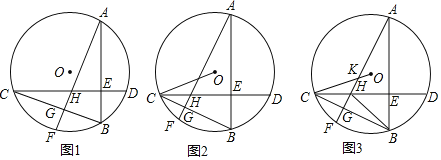
【題目】已知:點![]() 在
在![]() 上,弦
上,弦![]() ,垂足
,垂足![]() ,弦
,弦![]() ,垂足為
,垂足為![]() ,弦
,弦![]() 與
與![]() 相交于點
相交于點![]() ;
;
(1)如圖![]() ,求證:
,求證:![]() ;
;
(2)如圖![]() ,連接
,連接![]() ,當
,當![]() 平分
平分![]() 時,求證:弧
時,求證:弧![]() 弧
弧![]() ;
;
(3)如圖![]() ,在(2)的條件下,半徑
,在(2)的條件下,半徑![]() 與
與![]() 相交于點
相交于點![]() ,連接
,連接![]() ,若
,若![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
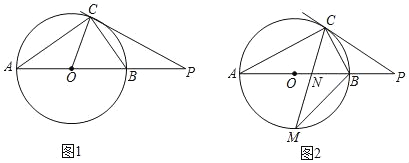
【題目】已知,AB是⊙O的直徑,點C在⊙O上,點P是AB延長線上一點,連接CP.
(1)如圖1,若∠PCB=∠A.
①求證:直線PC是⊙O的切線;
②若CP=CA,OA=2,求CP的長;
(2)如圖2,若點M是弧AB的中點,CM交AB于點N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車經銷商計劃投入7.1萬元購進100輛A型和30輛B型自行車,其中B型車單價是A型車單價的6倍少60元.
(1)求A、B兩種型號的自行車單價分別是多少元?
(2)后來由于該經銷商資金緊張,投入購車的資金不超過5.86萬元,但購進這批自行年的總數不變,那么至多能購進B型車多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解本學期初三期中調研測試數學試題的命題質量與難度系數,命題教師選取了一個水平相當的初三年級進行分析研究,隨機抽取部分學生成績(得分為整數,滿分為130分)分為5組:第一組55~70,第二組70~85,第三組85~100,第四組100~115,第五組115~130;統計后得到如圖所示的頻數分布直方圖(每組含最小值不含最大值)和扇形統計圖,觀察圖形的信息,回答下列問題:
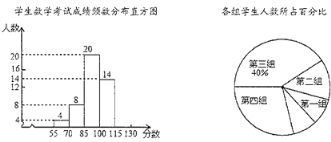
(1)本次調查共隨機抽取了該年級多少名學生?并將頻數分布直方圖補充完整;
(2)若將得分轉化為等級,規定:得分低于70分評為“D”,70~100分評為“C”,100~115分評為“B”,115~130分評為“A”,那么該年級1500名考生中,考試成績評為“B”的學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 圖象的一部分如圖所示,給出以下結論:
圖象的一部分如圖所示,給出以下結論:![]() ;
;![]() 當
當![]() 時,函數有最大值;
時,函數有最大值;![]() 方程
方程![]() 的解是
的解是![]() ,
,![]() ;
;![]() ,其中結論錯誤的個數是
,其中結論錯誤的個數是![]()
![]()
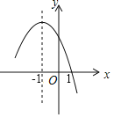
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某樓盤準備以每平方米15000元的均價對外銷售,由于國務院有關房地產的新政策出臺后,購房者持幣觀望,房地產開發商為了加快資金周轉,對價格經過兩次下調后,決定以每平方米12150元的均價開盤銷售
![]() 求平均每次下調的百分率.
求平均每次下調的百分率.
![]() 某人準備以開盤價均價購買一套100平方米的住房,開發商給予以下兩種優惠方案以供選擇:
某人準備以開盤價均價購買一套100平方米的住房,開發商給予以下兩種優惠方案以供選擇:
![]() 打
打![]() 折銷售;
折銷售;![]() 不打折,一次性送裝修費每平方米250元.
不打折,一次性送裝修費每平方米250元.
試問哪種方案更優惠?比另外一種方案優惠多少元?![]() 不考慮其他因素
不考慮其他因素![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com