
【題目】定義:三角形一邊上的點(diǎn)將該邊分為兩條線段,且這兩條線段的積等于這個(gè)點(diǎn)到該邊所對頂點(diǎn)連線的平方,則稱這個(gè)點(diǎn)為三角形該邊的“好點(diǎn)”.如圖1,△ABC中,點(diǎn)D是BC邊上一點(diǎn),連結(jié)AD,若![]() ,則稱點(diǎn)D是△ABC中BC邊上的“好點(diǎn)”.
,則稱點(diǎn)D是△ABC中BC邊上的“好點(diǎn)”.
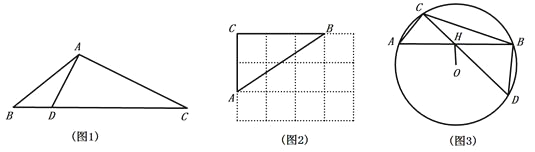
(1)如圖2,△ABC的頂點(diǎn)是![]() 網(wǎng)格圖的格點(diǎn),請僅用直尺畫出AB邊上的一個(gè)“好點(diǎn)”.
網(wǎng)格圖的格點(diǎn),請僅用直尺畫出AB邊上的一個(gè)“好點(diǎn)”.
(2)△ABC中,BC=9,![]() ,
,![]() ,點(diǎn)D是BC邊上的“好點(diǎn)”,求線段BD的長.
,點(diǎn)D是BC邊上的“好點(diǎn)”,求線段BD的長.
(3)如圖3,△ABC是![]() 的內(nèi)接三角形,OH⊥AB于點(diǎn)H,連結(jié)CH并延長交
的內(nèi)接三角形,OH⊥AB于點(diǎn)H,連結(jié)CH并延長交![]() 于點(diǎn)D.
于點(diǎn)D.
①求證:點(diǎn)H是△BCD中CD邊上的“好點(diǎn)”.
②若![]() 的半徑為9,∠ABD=90°,OH=6,請直接寫出
的半徑為9,∠ABD=90°,OH=6,請直接寫出![]() 的值.
的值.
【答案】(1)詳見解析;(2)![]() 或5;(3)①詳見解析;②
或5;(3)①詳見解析;②![]() .
.
【解析】
(1)作AB邊上的垂線或中線即可;
(2)作AE⊥BC于點(diǎn)E,根據(jù)三角函數(shù)求出BE、CE、AE的長,設(shè)DE為a,分①若點(diǎn)D在點(diǎn)E左側(cè)②若點(diǎn)D在點(diǎn)E右側(cè),根據(jù)“好點(diǎn)”的定義進(jìn)行求解即可;
(3)①根據(jù)“同弧或等弧所對的圓周角相等”證△AHC∽△DHB,再根據(jù)“好點(diǎn)”的定義判斷即可;
②連接AD,根據(jù)∠ABD=90°判斷AD為直徑,用勾股定理求出AH的長,再根據(jù)勾股定理求出DH的長,根據(jù)①中的結(jié)論求出CH的長即可求得比值.
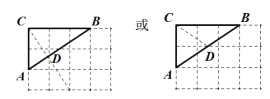
(1)如圖所示:D點(diǎn)及為AB邊上的“好點(diǎn)”
(2)作AE⊥BC于點(diǎn)E,由![]() ,
,![]() 可設(shè)AE=4x,
可設(shè)AE=4x,
則BE=3x,CE=6x,
∴BC=9x=9,∴![]() ,
,
∴BE=3,CE=6,AE=4,
設(shè)DE=a,
①若點(diǎn)D在點(diǎn)E左側(cè),
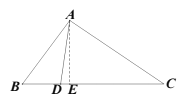
由點(diǎn)D是BC邊上的“好點(diǎn)”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.
②若點(diǎn)D在點(diǎn)E右側(cè),
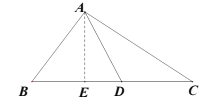
由點(diǎn)D是BC邊上的“好點(diǎn)”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去)
(舍去)
∴![]() .
.
∴![]() 或5.
或5.
(3)①∵∠CHA=∠BHD,∠ACH=∠DBH
∴△AHC∽△DHB
∴![]() ,即
,即![]()
∵OH⊥AB
∴AH=BH
∴![]()
∴點(diǎn)H是△BCD中CD邊上的“好點(diǎn)”.
②連接AD.
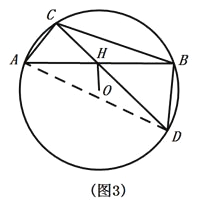
∵∠ABD=90°
∴AD為直徑,
∵OH⊥AB,OH=6
∴![]() ,BD=2OH=12
,BD=2OH=12
∴BH=AH=![]()
∴![]()
由①得:![]()
即![]()
∴CH=![]()
∴![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
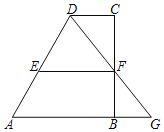
【題目】如圖,四邊形ABCD中,AB∥CD,CD≠AB,點(diǎn)F在BC上,連DF與AB的延長線交于點(diǎn)G.
(1)求證:CFFG=DFBF;
(2)當(dāng)點(diǎn)F是BC的中點(diǎn)時(shí),過F作EF∥CD交AD于點(diǎn)E,若AB=12,EF=8,求CD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(本題滿分8分)一個(gè)不透明的口袋中裝有2個(gè)紅球(記為紅球1、紅球2)、1個(gè)白球、1個(gè)黑球,這些球除顏色外都相同,將球搖勻.
(1)從中任意摸出1個(gè)球,恰好摸到紅球的概率是 ;
(2)先從中任意摸出1個(gè)球,再從余下的3個(gè)球中任意摸出1個(gè)球,請用列舉法(畫樹狀圖或列表)求兩次都摸到紅球的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(問題呈現(xiàn))阿基米德折弦定理:
如圖1,AB和BC是⊙O的兩條弦(即折線ABC是圓的一條折弦),BC>AB,點(diǎn)M是![]() 的中點(diǎn),則從M向BC所作垂線的垂足D是折弦ABC的中點(diǎn),即CD=DB+BA.下面是運(yùn)用“截長法”證明CD=DB+BA的部分證明過程.
的中點(diǎn),則從M向BC所作垂線的垂足D是折弦ABC的中點(diǎn),即CD=DB+BA.下面是運(yùn)用“截長法”證明CD=DB+BA的部分證明過程.
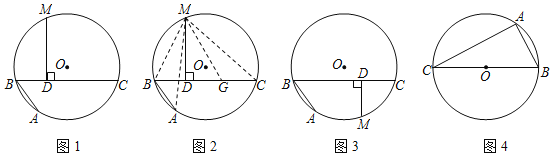
證明:如圖2,在CD上截取CG=AB,連接MA、MB、MC和MG.
∵M是![]() 的中點(diǎn),
的中點(diǎn),
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根據(jù)證明過程,分別寫出下列步驟的理由:
① ,
② ,
③ ;
(理解運(yùn)用)如圖1,AB、BC是⊙O的兩條弦,AB=4,BC=6,點(diǎn)M是![]() 的中點(diǎn),MD⊥BC于點(diǎn)D,則BD= ;
的中點(diǎn),MD⊥BC于點(diǎn)D,則BD= ;
(變式探究)如圖3,若點(diǎn)M是![]() 的中點(diǎn),(問題呈現(xiàn))中的其他條件不變,判斷CD、DB、BA之間存在怎樣的數(shù)量關(guān)系?并加以證明.
的中點(diǎn),(問題呈現(xiàn))中的其他條件不變,判斷CD、DB、BA之間存在怎樣的數(shù)量關(guān)系?并加以證明.
(實(shí)踐應(yīng)用)根據(jù)你對阿基米德折弦定理的理解完成下列問題:
如圖4,BC是⊙O的直徑,點(diǎn)A圓上一定點(diǎn),點(diǎn)D圓上一動(dòng)點(diǎn),且滿足∠DAC=45°,若AB=6,⊙O的半徑為5,求AD長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
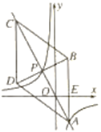
【題目】如圖,在平面直角坐標(biāo)系xOy中,菱形ABCD的對角線AC與BD交于點(diǎn)P(-1,2),AB⊥x軸于點(diǎn)E,正比例函數(shù)y=mx的圖像與反比例函數(shù)![]() 的圖像相交于A,P兩點(diǎn)。
的圖像相交于A,P兩點(diǎn)。
(1)求m,n的值與點(diǎn)A的坐標(biāo);
(2)求證:![]() ∽
∽![]()
(3)求![]() 的值
的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中的兩個(gè)圖形
中的兩個(gè)圖形![]() 與
與![]() ,給出如下定義:
,給出如下定義:![]() 為圖形
為圖形![]() 上任意一點(diǎn),
上任意一點(diǎn),![]() 為圖形
為圖形![]() 上任意一點(diǎn),如果
上任意一點(diǎn),如果![]() 兩點(diǎn)間的距離有最小值,那么稱這個(gè)最小值為圖形
兩點(diǎn)間的距離有最小值,那么稱這個(gè)最小值為圖形![]() 間的“和睦距離”,記作
間的“和睦距離”,記作![]() ,若圖形
,若圖形![]() 有公共點(diǎn),則
有公共點(diǎn),則![]() .
.
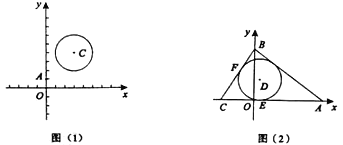
(1)如圖(1),![]() ,
,![]() ,⊙
,⊙![]() 的半徑為2,則
的半徑為2,則![]() ,
,![]() ;
;
(2)如圖(2),已知![]() 的一邊
的一邊![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() .
.
①![]() 是
是![]() 內(nèi)一點(diǎn),若
內(nèi)一點(diǎn),若![]() 、
、![]() 分別且⊙
分別且⊙![]() 于E、F,且
于E、F,且![]() ,判斷
,判斷![]() 與⊙
與⊙![]() 的位置關(guān)系,并求出
的位置關(guān)系,并求出![]() 點(diǎn)的坐標(biāo);
點(diǎn)的坐標(biāo);
②若以![]() 為半徑,①中的
為半徑,①中的![]() 為圓心的⊙
為圓心的⊙![]() ,有
,有![]() ,
,![]() ,直接寫出
,直接寫出![]() 的取值范圍 .
的取值范圍 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知⊙O是等腰Rt△ABC的外接圓,點(diǎn)D是![]() 上一點(diǎn),BD交AC于點(diǎn)E,若BC=4,AD=
上一點(diǎn),BD交AC于點(diǎn)E,若BC=4,AD=![]() ,則AE的長是( )
,則AE的長是( )
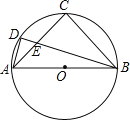
A. 1 B. 1.2 C. 2 D. 3
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
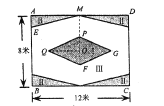
【題目】如圖,某校準(zhǔn)備給長12米,寬8米的矩形![]() 室內(nèi)場地進(jìn)行地面裝飾,現(xiàn)將其劃分為區(qū)域Ⅰ(菱形
室內(nèi)場地進(jìn)行地面裝飾,現(xiàn)將其劃分為區(qū)域Ⅰ(菱形![]() ),區(qū)域Ⅱ(4個(gè)全等的直角三角形),剩余空白部分記為區(qū)域Ⅲ;點(diǎn)
),區(qū)域Ⅱ(4個(gè)全等的直角三角形),剩余空白部分記為區(qū)域Ⅲ;點(diǎn)![]() 為矩形和菱形的對稱中心,
為矩形和菱形的對稱中心,![]() ,
,![]() ,
,![]() ,為了美觀,要求區(qū)域Ⅱ的面積不超過矩形
,為了美觀,要求區(qū)域Ⅱ的面積不超過矩形![]() 面積的
面積的![]() ,若設(shè)
,若設(shè)![]() 米.
米.
甲 | 乙 | 丙 | |
單價(jià)(元/米2) |
|
|
|
(1)當(dāng)![]() 時(shí),求區(qū)域Ⅱ的面積.
時(shí),求區(qū)域Ⅱ的面積.
(2)計(jì)劃在區(qū)域Ⅰ,Ⅱ分別鋪設(shè)甲,乙兩款不同的深色瓷磚,區(qū)域Ⅲ鋪設(shè)丙款白色瓷磚,
①在相同光照條件下,當(dāng)場地內(nèi)白色區(qū)域的面積越大,室內(nèi)光線亮度越好.當(dāng)![]() 為多少時(shí),室內(nèi)光線亮度最好,并求此時(shí)白色區(qū)域的面積.
為多少時(shí),室內(nèi)光線亮度最好,并求此時(shí)白色區(qū)域的面積.
②三種瓷磚的單價(jià)列表如下,![]() 均為正整數(shù),若當(dāng)
均為正整數(shù),若當(dāng)![]() 米時(shí),購買三款瓷磚的總費(fèi)用最少,且最少費(fèi)用為7200元,此時(shí)
米時(shí),購買三款瓷磚的總費(fèi)用最少,且最少費(fèi)用為7200元,此時(shí)![]() __________,
__________,
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
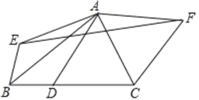
【題目】如圖,△ABC中,∠BAC=75°,BC=7,△ABC的面積為14,D為 BC邊上一動(dòng)點(diǎn)(不與B,C重合),將△ABD和△ACD分別沿直線AB,AC翻折得到△ABE與△ACF,那么△AEF的面積最小值為_____.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com