
【題目】在平面直角坐標系![]() 中的兩個圖形
中的兩個圖形![]() 與
與![]() ,給出如下定義:
,給出如下定義:![]() 為圖形
為圖形![]() 上任意一點,
上任意一點,![]() 為圖形
為圖形![]() 上任意一點,如果
上任意一點,如果![]() 兩點間的距離有最小值,那么稱這個最小值為圖形
兩點間的距離有最小值,那么稱這個最小值為圖形![]() 間的“和睦距離”,記作
間的“和睦距離”,記作![]() ,若圖形
,若圖形![]() 有公共點,則
有公共點,則![]() .
.
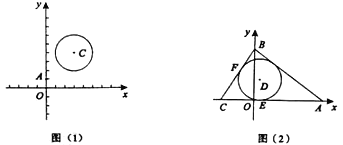
(1)如圖(1),![]() ,
,![]() ,⊙
,⊙![]() 的半徑為2,則
的半徑為2,則![]() ,
,![]() ;
;
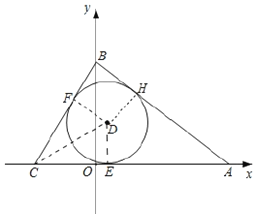
(2)如圖(2),已知![]() 的一邊
的一邊![]() 在
在![]() 軸上,
軸上,![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() .
.
①![]() 是
是![]() 內一點,若
內一點,若![]() 、
、![]() 分別且⊙
分別且⊙![]() 于E、F,且
于E、F,且![]() ,判斷
,判斷![]() 與⊙
與⊙![]() 的位置關系,并求出
的位置關系,并求出![]() 點的坐標;
點的坐標;
②若以![]() 為半徑,①中的
為半徑,①中的![]() 為圓心的⊙
為圓心的⊙![]() ,有
,有![]() ,
,![]() ,直接寫出
,直接寫出![]() 的取值范圍 .
的取值范圍 .
【答案】(1)2,![]() ;(2)①
;(2)①![]() 是⊙
是⊙![]() 的切線,
的切線,![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)根據圖形M,N間的“和睦距離”的定義結合已知條件求解即可.
(2)①連接DF,DE,作DH⊥AB于H.設OC=x.首先證明∠CBO=30![]() ,再證明DH=DE即可證明
,再證明DH=DE即可證明![]() 是⊙
是⊙![]() 的切線,再求出OE,DE的長即可求出點D的坐標.
的切線,再求出OE,DE的長即可求出點D的坐標.
②根據![]() ,
,![]() 得到不等式組解決問題即可.
得到不等式組解決問題即可.
(1)∵A(0,1),C(3,4),⊙C的半徑為2,
∴d(C,⊙C)=2,
d(O,⊙C)=AC2=![]() ,
,
故答案為2;![]() ;
;
(2)①連接![]() ,作
,作![]() 于
于![]() .設
.設![]() .
.
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 是⊙
是⊙![]() 的切線,
的切線,
∴![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切線.
的切線.
∵![]() ,
,
設![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
②∵![]()
∴B(0,![]() )
)
∴BD=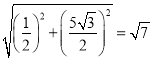
由![]() ,
,![]() ,
,![]() 得
得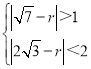
解得![]() 或
或![]()
故答案為:![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A、B、C、D是⊙O上的四個點,AD是⊙O的直徑,過點C的切線與AB的延長線垂直于點E,連接AC、BD相交于點F.
(1)求證:AC平分∠BAD;
(2)若⊙O的半徑為![]() ,AC=6,求DF的長.
,AC=6,求DF的長.
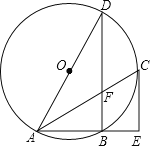
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC⊥AB,BC交⊙O于點D,點E在劣弧BD上,DE的延長線交AB的延長線于點F,連接AE交BD于點G.
(1)求證:∠AED=∠CAD;
(2)若點E是劣弧BD的中點,求證:ED2=EGEA;
(3)在(2)的條件下,若BO=BF,DE=2,求EF的長.
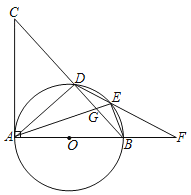
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,點C、D、B、F在一條直線上,且AB⊥BD,DE⊥BD,AB=CD,CE=AF.
求證:(1)△ABF≌△CDE;
(2)CE⊥AF.
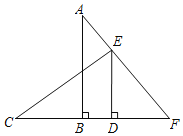
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:三角形一邊上的點將該邊分為兩條線段,且這兩條線段的積等于這個點到該邊所對頂點連線的平方,則稱這個點為三角形該邊的“好點”.如圖1,△ABC中,點D是BC邊上一點,連結AD,若![]() ,則稱點D是△ABC中BC邊上的“好點”.
,則稱點D是△ABC中BC邊上的“好點”.
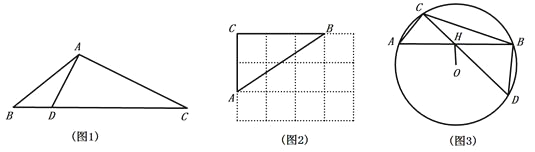
(1)如圖2,△ABC的頂點是![]() 網格圖的格點,請僅用直尺畫出AB邊上的一個“好點”.
網格圖的格點,請僅用直尺畫出AB邊上的一個“好點”.
(2)△ABC中,BC=9,![]() ,
,![]() ,點D是BC邊上的“好點”,求線段BD的長.
,點D是BC邊上的“好點”,求線段BD的長.
(3)如圖3,△ABC是![]() 的內接三角形,OH⊥AB于點H,連結CH并延長交
的內接三角形,OH⊥AB于點H,連結CH并延長交![]() 于點D.
于點D.
①求證:點H是△BCD中CD邊上的“好點”.
②若![]() 的半徑為9,∠ABD=90°,OH=6,請直接寫出
的半徑為9,∠ABD=90°,OH=6,請直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
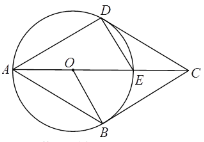
【題目】如圖,已知四邊形ABCD中,E是對角線AC上一點,DE=EC,以AE為直徑的⊙O與CD相切于點D,點B在⊙O上,連接OB.
(1)求證:DE=OE;
(2)若CD∥AB,求證:BC是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 的半徑為 4,
的半徑為 4,![]() 是圓的直徑,點
是圓的直徑,點![]() 是
是![]() 的切線
的切線![]() 上的一個動點,連接
上的一個動點,連接![]() 交
交![]() 于點
于點![]() ,弦
,弦![]() 平行于
平行于![]() ,連接
,連接![]() .
.

(1)試判斷直線![]() 與
與![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)當![]() __________時,四邊形
__________時,四邊形![]() 為菱形;
為菱形;
(3)當![]() ___________時,四邊形
___________時,四邊形![]() 為正方形.
為正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是長為10m,傾斜角為30°的自動扶梯,平臺BD與大樓CE垂直,且與扶梯AB的長度相等,在B處測得大樓頂部C的仰角為65°,求大樓CE的高度(結果保留整數).(參考數據:sin65°=0.90,tan65°=2.14)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com