
【題目】紅樹(shù)林學(xué)校在七年級(jí)新生中舉行了全員參加的“防溺水”安全知識(shí)競(jìng)賽,試卷題目共10題,每題10分.現(xiàn)分別從三個(gè)班中各隨機(jī)取10名同學(xué)的成績(jī)(單位:分),收集數(shù)據(jù)如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理數(shù)據(jù):
分?jǐn)?shù) 人數(shù) 班級(jí) | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析數(shù)據(jù):
平均數(shù) | 中位數(shù) | 眾數(shù) | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根據(jù)以上信息回答下列問(wèn)題:
(1)請(qǐng)直接寫出表格中![]() 的值;
的值;
(2)比較這三組樣本數(shù)據(jù)的平均數(shù)、中位數(shù)和眾數(shù),你認(rèn)為哪個(gè)班的成績(jī)比較好?請(qǐng)說(shuō)明理由;
(3)為了讓學(xué)生重視安全知識(shí)的學(xué)習(xí),學(xué)校將給競(jìng)賽成績(jī)滿分的同學(xué)頒發(fā)獎(jiǎng)狀,該校七年級(jí)新生共570人,試估計(jì)需要準(zhǔn)備多少?gòu)埅?jiǎng)狀?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)2班成績(jī)比較好;理由見(jiàn)解析;(3)估計(jì)需要準(zhǔn)備76張獎(jiǎng)狀.
;(2)2班成績(jī)比較好;理由見(jiàn)解析;(3)估計(jì)需要準(zhǔn)備76張獎(jiǎng)狀.
【解析】
(1)根據(jù)眾數(shù)和中位數(shù)的概念求解可得;
(2)分別從平均數(shù)、眾數(shù)和中位數(shù)三個(gè)方面比較大小即可得;
(3)利用樣本估計(jì)總體思想求解可得.
(1)由題意知![]() ,
,
![]() ,
,
2班成績(jī)重新排列為60,70,80,80,80,90,90,90,90,100,
∴![]() ;
;
(2)從平均數(shù)上看三個(gè)班都一樣;
從中位數(shù)看,1班和3班一樣是80,2班最高是85;
從眾數(shù)上看,1班和3班都是80,2班是90;
綜上所述,2班成績(jī)比較好;
(3)![]() (張),
(張),
答:估計(jì)需要準(zhǔn)備76張獎(jiǎng)狀.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:在平面直角坐標(biāo)系中,點(diǎn)![]() 的橫、縱坐標(biāo)的絕對(duì)值之和叫做點(diǎn)
的橫、縱坐標(biāo)的絕對(duì)值之和叫做點(diǎn)![]() 的勾股值,記
的勾股值,記![]()
![]() .若拋物線
.若拋物線![]() 與直線
與直線![]() 只有一個(gè)交點(diǎn)
只有一個(gè)交點(diǎn)![]() ,已知點(diǎn)
,已知點(diǎn)![]() 在第一象限,且
在第一象限,且![]() ,令
,令![]() ,則
,則![]() 的取值范圍為( )
的取值范圍為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
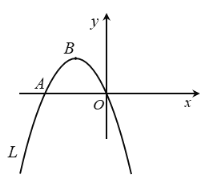
【題目】如圖,拋物線![]()
![]() 經(jīng)過(guò)原點(diǎn)和點(diǎn)
經(jīng)過(guò)原點(diǎn)和點(diǎn)![]() ,頂點(diǎn)為
,頂點(diǎn)為![]() ,拋物線
,拋物線![]() 與拋物線
與拋物線![]() 關(guān)于原點(diǎn)
關(guān)于原點(diǎn)![]() 對(duì)稱.
對(duì)稱.
(1)求拋物線![]() 的函數(shù)表達(dá)式及點(diǎn)
的函數(shù)表達(dá)式及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)已知點(diǎn)![]() 、
、![]() 在拋物線
在拋物線![]() 上的對(duì)應(yīng)點(diǎn)分別為
上的對(duì)應(yīng)點(diǎn)分別為![]() 、
、![]() ,
,![]() 的對(duì)稱軸交
的對(duì)稱軸交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,則拋物線
,則拋物線![]() 的對(duì)稱軸上是否存在點(diǎn)
的對(duì)稱軸上是否存在點(diǎn)![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點(diǎn)的三角形與
為頂點(diǎn)的三角形與![]() 相似?若存在,請(qǐng)求出點(diǎn)
相似?若存在,請(qǐng)求出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
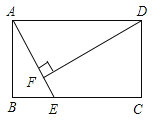
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 邊上的一個(gè)動(dòng)點(diǎn),連接
邊上的一個(gè)動(dòng)點(diǎn),連接![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 于
于![]() ,連接
,連接![]() ,當(dāng)
,當(dāng)![]() 為等腰三角形時(shí),則
為等腰三角形時(shí),則![]() 的長(zhǎng)是_____________.
的長(zhǎng)是_____________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:兩個(gè)相似等腰三角形,如果它們的底角有一個(gè)公共的頂點(diǎn),那么把這兩個(gè)三角形稱為“關(guān)聯(lián)等腰三角形”.如圖,在![]() 與
與![]() 中,
中,![]() ,且
,且![]() 所以稱
所以稱![]() 與
與![]() 為“關(guān)聯(lián)等腰三角形”,設(shè)它們的頂角為
為“關(guān)聯(lián)等腰三角形”,設(shè)它們的頂角為![]() ,連接
,連接![]() ,則稱
,則稱![]() 會(huì)為“關(guān)聯(lián)比".
會(huì)為“關(guān)聯(lián)比".
下面是小穎探究“關(guān)聯(lián)比”與α之間的關(guān)系的思維過(guò)程,請(qǐng)閱讀后,解答下列問(wèn)題:
[特例感知]
![]() 當(dāng)
當(dāng)![]() 與
與![]() 為“關(guān)聯(lián)等腰三角形”,且
為“關(guān)聯(lián)等腰三角形”,且![]() 時(shí),
時(shí),
①在圖1中,若點(diǎn)![]() 落在
落在![]() 上,則“關(guān)聯(lián)比”
上,則“關(guān)聯(lián)比”![]() =
=
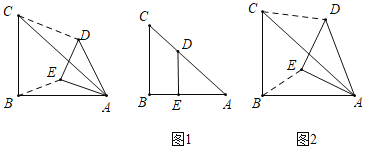
②在圖2中,探究![]() 與
與![]() 的關(guān)系,并求出“關(guān)聯(lián)比”
的關(guān)系,并求出“關(guān)聯(lián)比”![]() 的值.
的值.

[類比探究]
![]() 如圖3,
如圖3,
①當(dāng)![]() 與
與![]() 為“關(guān)聯(lián)等腰三角形”,且
為“關(guān)聯(lián)等腰三角形”,且![]() 時(shí),“關(guān)聯(lián)比”
時(shí),“關(guān)聯(lián)比”![]() =
=
②猜想:當(dāng)![]() 與
與![]() 為“關(guān)聯(lián)等腰三角形”,且
為“關(guān)聯(lián)等腰三角形”,且![]() 時(shí),“關(guān)聯(lián)比”
時(shí),“關(guān)聯(lián)比”![]() = (直接寫出結(jié)果,用含
= (直接寫出結(jié)果,用含![]() 的式子表示)
的式子表示)
[遷移運(yùn)用]
![]() 如圖4,
如圖4, ![]() 與
與![]() 為“關(guān)聯(lián)等腰三角形”.若
為“關(guān)聯(lián)等腰三角形”.若![]() 點(diǎn)
點(diǎn)![]() 為
為![]() 邊上一點(diǎn),且
邊上一點(diǎn),且![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 上一動(dòng)點(diǎn),求點(diǎn)
上一動(dòng)點(diǎn),求點(diǎn)![]() 自點(diǎn)
自點(diǎn)![]() 運(yùn)動(dòng)至點(diǎn)
運(yùn)動(dòng)至點(diǎn)![]() 時(shí),點(diǎn)
時(shí),點(diǎn)![]() 所經(jīng)過(guò)的路徑長(zhǎng).
所經(jīng)過(guò)的路徑長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
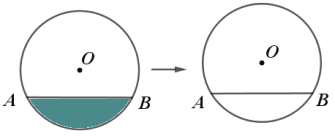
【題目】如圖,![]() 是一個(gè)圓柱體污水管道的橫截面,管道中有部分污水,污水液面橫截面寬度(即
是一個(gè)圓柱體污水管道的橫截面,管道中有部分污水,污水液面橫截面寬度(即![]() 長(zhǎng))為
長(zhǎng))為![]() 污水管道直徑為
污水管道直徑為![]() 則弦
則弦![]() 所對(duì)圓周角的大小為_____________________
所對(duì)圓周角的大小為_____________________![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在![]() 中,
中,![]() 點(diǎn)
點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)以
出發(fā)以![]() 的速度沿折線
的速度沿折線![]() 運(yùn)動(dòng),點(diǎn)
運(yùn)動(dòng),點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)以
出發(fā)以![]() 的速度沿
的速度沿![]() 運(yùn)動(dòng),
運(yùn)動(dòng),![]() 兩點(diǎn)同時(shí)出發(fā),當(dāng)某一點(diǎn)運(yùn)動(dòng)到點(diǎn)
兩點(diǎn)同時(shí)出發(fā),當(dāng)某一點(diǎn)運(yùn)動(dòng)到點(diǎn)![]() 時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng)設(shè)運(yùn)動(dòng)時(shí)間為
時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng)設(shè)運(yùn)動(dòng)時(shí)間為![]() 的面積為
的面積為![]() 關(guān)于
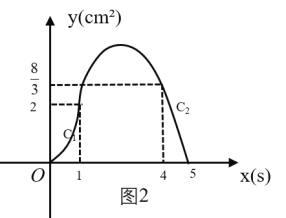
關(guān)于![]() 的函數(shù)圖像由
的函數(shù)圖像由![]() 兩段組成,如圖2所示.
兩段組成,如圖2所示.
(1)求![]() 的值;
的值;
(2)求圖2中圖像![]() 段的函數(shù)表達(dá)式;
段的函數(shù)表達(dá)式;
(3)當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到線段
運(yùn)動(dòng)到線段![]() 上某一段時(shí),
上某一段時(shí),![]() 的面積大于當(dāng)點(diǎn)
的面積大于當(dāng)點(diǎn)![]() 在線段
在線段![]() 上任意一點(diǎn)時(shí)
上任意一點(diǎn)時(shí)![]() 的面積,求
的面積,求![]() 的取值范圍.(直接寫出答案)
的取值范圍.(直接寫出答案)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】“普洱茶”是云南有名的特產(chǎn),某網(wǎng)店專門銷售某種品牌的普洱茶,成本為30元/盒,每天銷售![]() (件)與銷售單價(jià)
(件)與銷售單價(jià)![]() (元)之間存在一次函數(shù)關(guān)系,如圖所示.
(元)之間存在一次函數(shù)關(guān)系,如圖所示.
(1)求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)如果規(guī)定每天該種普洱茶的銷售量不低于240盒,該網(wǎng)店店主熱心公益事業(yè),決定從每天的銷售利潤(rùn)中捐出500元給扶貧基金會(huì),當(dāng)銷售單價(jià)為多少元時(shí),每天獲取的凈利潤(rùn)最大,最大凈利潤(rùn)是多少?(注:凈利潤(rùn)=總利潤(rùn)-捐款)
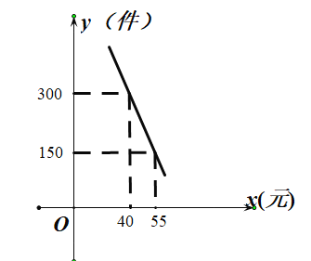
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
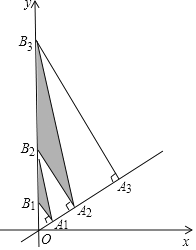
【題目】如圖,直線![]() 上有點(diǎn)
上有點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別過(guò)點(diǎn)
分別過(guò)點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 作直線
作直線![]() 的垂線,交
的垂線,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,依次連接
,依次連接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,得到
,得到![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() 的面積為_______.(用含有正整數(shù)
的面積為_______.(用含有正整數(shù)![]() 的式子表示)
的式子表示)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com