
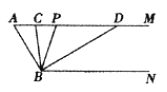
【題目】如圖,已知AM//BN,∠A=600.點P是射線AM上一動點(與點A不重合),BC、BD分別平分∠ABP和∠PBN,分別交射線AM于點C,D.
(1)①∠ABN的度數是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度數;
(3)當點P運動時,∠APB與∠ADB之間的數量關系是否隨之發生變化?若不變化,請寫出它們之間的關系,并說明理由;若變化,請寫出變化規律.
(4)當點P運動到使∠ACB=∠ABD時,∠ABC的度數是 .
【答案】(1)①120°;②∠CBN;(2)60°;(3)答案見解析;(4)30°.
【解析】
(1)①根據兩直線平行,同旁內角互補即可求得答案;
②根據兩直線平行,內錯角相等即可得答案;
(2)由(1)知∠ABP+∠PBN=120°,繼而結合角平分線的定義可得2∠CBP+2∠DBP=120°,進而可求得答案;
(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根據BD平分∠PBN知∠PBN=2∠DBN,從而可得∠APB:∠ADB=2:1;
(4)由AM∥BN得∠ACB=∠CBN,當∠ACB=∠ABD時有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根據∠ABN=120°,∠CBD=60°可得答案.
(1)①∵AM∥BN,∠A=60°,
∴∠A+∠ABN=180°,
∴∠ABN=120°;
②∵AM∥BN,
∴∠ACB=∠CBN,
故答案為:①120°;②∠CBN;
(2)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°;
(3)不變,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(4)∵AM∥BN,
∴∠ACB=∠CBN,
當∠ACB=∠ABD時,則有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°,
故答案為:30°.


科目:初中數學 來源: 題型:
【題目】已知點O是正方形ABCD對角線BD的中點.
(1)如圖1,若點E是OD的中點,點F是AB上一點,且使得∠CEF=90°,過點E作ME∥AD,交AB于點M,交CD于點N.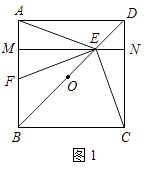
①∠AEM=∠FEM; ②點F是AB的中點;
(2)如圖2,若點E是OD上一點,點F是AB上一點,且使 ![]() =
= ![]() =
= ![]() ,請判斷△EFC的形狀,并說明理由;
,請判斷△EFC的形狀,并說明理由;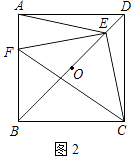
(3)如圖3,若E是OD上的動點(不與O,D重合),連接CE,過E點作EF⊥CE,交AB于點F,當 ![]() =
= ![]() 時,請猜想
時,請猜想 ![]() 的值(請直接寫出結論).
的值(請直接寫出結論).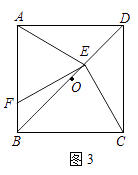
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把四張形狀大小完全相同的小長方形卡片(如圖①)不重疊地放在一個底面為長方形(長為m,寬為n)的盒子底部(如圖②),盒子底面未被卡片覆蓋的部分用陰影表示.則圖②中兩塊陰影部分的周長和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 點A1在AD邊上,A1B1與BD交于點E,D1B1與CD交于點F.
(1)求證:四邊形EB1FD是平行四邊形;
(2)若AB=3,BC=4,AA1=1,求B1F的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=kx+b與反比例函數y= ![]() (x<0)的圖象交于點A(﹣1,m),與x軸交于點B(1,0)
(x<0)的圖象交于點A(﹣1,m),與x軸交于點B(1,0)
(1)求m的值;
(2)求直線AB的解析式;
(3)若直線x=t(t>1)與直線y=kx+b交于點M,與x軸交于點N,連接AN,S△AMN= ![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點O在直線MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 則∠BOC=_______,∠AOM=_______,∠BON=_________;
則∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 則∠BON=_______(用含有
則∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)將∠AOB繞著點O順時針轉到圖2的位置,其他條件不變,若∠AOC=![]() (
(![]() 為鈍角),求∠BON的度數(用含
為鈍角),求∠BON的度數(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BF是⊙O的直徑,A為⊙O上(異于B、F)一點,⊙O的切線MA與FB的延長線交于點M;P為AM上一點,PB的延長線交⊙O于點C,D為BC上一點且PA=PD,AD的延長線交⊙O于點E.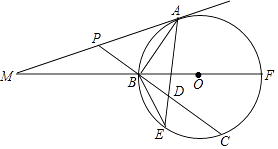
(1)求證: ![]() =
= ![]() ;
;
(2)若ED、EA的長是一元二次方程x2﹣5x+5=0的兩根,求BE的長;
(3)若MA=6 ![]() ,sin∠AMF=
,sin∠AMF= ![]() ,求AB的長.
,求AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com