
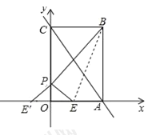
【題目】如圖,把矩形![]() 放入平面直角坐標系
放入平面直角坐標系![]() 中,使
中,使![]() 分別落在
分別落在![]() 軸的正半軸上,其中
軸的正半軸上,其中![]() ,對角線
,對角線![]() 所在直線解析式為
所在直線解析式為![]() ,將矩形
,將矩形![]() 沿著
沿著![]() 折疊,使點
折疊,使點![]() 落在邊
落在邊![]() 上的
上的![]() 處.
處.

(1)求點![]() 的坐標;
的坐標;
(2)求![]() 的長度;
的長度;
(3)點![]() 是
是![]() 軸上一動點,是否存在點
軸上一動點,是否存在點![]() 使得
使得![]() 的周長最小,若存在,請求出點
的周長最小,若存在,請求出點![]() 的坐標,如不存在,請說明理由.
的坐標,如不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,見解析.
,見解析.
【解析】
(1)根據點C的坐標確定b的值,利用待定系數法求出點A坐標即可解決問題;
(2)在Rt△BCD中,BC=6,BD=AB=10, CD=![]() =8, OD=10-8=2,設DE=AE=x,在Rt△DEO中,根據DE2=OD2+OE2,構建方程即可解決問題;
=8, OD=10-8=2,設DE=AE=x,在Rt△DEO中,根據DE2=OD2+OE2,構建方程即可解決問題;
(3)如圖作點E關于y軸的對稱點E′,連接BE′交y軸于P,此時△BPE的周長最小.利用待定系數法求出直線BE′的解析式即可解決問題;
解:![]() ,四邊形
,四邊形![]() 是矩形,
是矩形,
![]()
![]() ,代入
,代入![]() 得到
得到![]()
![]() 直線
直線![]() 的解析式為
的解析式為![]()
令![]() ,得到
,得到
![]() .
.
![]() 在
在![]() 中,
中,![]()
![]() ,
,
![]()
設![]()
在![]() 中,
中, ![]()
![]()
![]()
![]()
![]() 如圖作點
如圖作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 交
交![]() 軸于
軸于![]() ,此時
,此時![]() 的周長最小.
的周長最小.
![]()
![]()
設直線![]() 的解析式為
的解析式為![]() ,則有
,則有 ,解得:
,解得:
![]() 直線
直線![]() 的解析式為
的解析式為![]()
![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,拋物線![]() 的圖像與x軸交于點A(3,0),與y軸交于點B,頂點C在直線
的圖像與x軸交于點A(3,0),與y軸交于點B,頂點C在直線![]() 上,將拋物線沿射線 AC的方向平移,
上,將拋物線沿射線 AC的方向平移,
當頂點C恰好落在y軸上的點D處時,點B落在點E處.
(1)求這個拋物線的解析式;
(2)求平移過程中線段BC所掃過的面積;
(3)已知點F在x軸上,點G在坐標平面內,且以點 C、E、F、G 為頂點的四邊形是矩形,求點F的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車在某次行駛過程中,油箱中的剩余油量y(升)與行駛路程x(千米)之間是一次函數關系,其部分圖象如圖所示.
(1)求y關于x的函數關系式;
(2)已知當油箱中的剩余油量為8升時,該汽車會開始提示加油.在此次行駛過程中,行駛了450千米時,司機發現離前方最近的加油站有75千米的路程.在開往該加油站的途中,當汽車開始提示加油時,離加油站的路程是多少千米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一點(不與點A、B重合),連接CO并延長CO交⊙O于點D,連接AD.
(1)AB=_____;
(2)當∠D=20°時,求∠BOD的度數.
(3)若△ACD與△BCO相似,求AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是一塊直角三角框,且∠C=90°,∠A=30°,現將圓心為點O的圓形紙片放置在三角框內部,將圓形紙片沿著三角框的內部邊緣滾動1周,回到起點位置時停止,若BC=9,圓形紙片的半徑為2,則圓心O運動的路徑長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)﹣24﹣11015
(2)﹣3×(﹣![]() )÷
)÷![]()
(3)(﹣![]() )÷
)÷![]()
(4)1÷(﹣1)+0÷4﹣5×0.1×(﹣2)3
(5)(﹣1)2009+(﹣2)3+2×(﹣3)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知線段AB=4cm,點C是直線AB上一點(不同于點A、B).下列說法:①若點C為線段AB的中點,則AC=2cm;②若AC=1cm,則點C為線段AB的四等分點;③若AC+BC=4cm,則點C一定在線段AB上;④若AC+BC>4cm,則點C一定在線段AB的延長線上;⑤若AC+BC=8cm,則AC=2cm.其中正確的個數有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半徑為6cm 的⊙O中,C,D為直徑AB 的三等分點,點E,F分別在AB兩側的半圓上,∠BCE =∠BDF = 60°,連結AE,BF.則圖中兩個陰影部分的面積和為 cm2.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一點,且
上一點,且![]() ,過點
,過點![]() 分別作
分別作![]() ,
,![]() ,垂足分別是
,垂足分別是![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() 是
是![]() 的中點;③
的中點;③![]() 垂直平分
垂直平分![]() ;④
;④![]() ;其中正確的個數為( )
;其中正確的個數為( )

A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com