
【題目】如圖,△ABC和△DEF均是邊長為4的等邊三角形,△DEF的頂點D為△ABC的一邊BC的中點,△DEF繞點D旋轉,且邊DF、DE始終分別交△ABC的邊AB、AC于點H、G.圖中直線BC兩側的圖形關于直線BC成軸對稱.連結HH′、HG、GG′、H′G′,其中HH′、GG′分別交BC于點I、J.
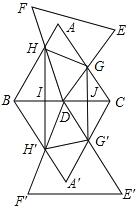
(1)求證:△DHB∽△GDC;
(2)設CG=x,四邊形HH′G′G的面積為y,
①求y關于x的函數解析式和自變量x的取值范圍;
②求當x為何值時,y的值最大,最大值為多少?
【答案】(1)證明見解析;(2)①y=![]() (
(![]() +
+![]() x)(4-
x)(4-![]() -
-![]() )(1≤x≤4);②x=2,y最大=4
)(1≤x≤4);②x=2,y最大=4![]() .
.
【解析】
試題分析:此題是幾何變換綜合題,主要考查相似三角形的性質和判定以及對稱的性質,用x表示線段是解決本題的關鍵,也是難點.
(1)由等邊三角形的特點得到相等關系,即可;
(2)由相似三角形得到![]() =
=![]() ,再結合對稱,表示出相關的線段,四邊形HH′G′G的面積為y求出即可.
,再結合對稱,表示出相關的線段,四邊形HH′G′G的面積為y求出即可.
試題解析:(1)在正△ABC中,∠ABC=∠ACB=60°,
∴∠BHD+∠BDH=120°,
在正△DEF中,∠EDF=60°,
∴∠GDC+∠BDH=120°,
∴∠BHD=∠GDC,
∴△DHB∽△GDC;
(2)①∵D為BC的中點,
∴BD=CD=2,
由△DHB∽△GDC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
得BH=![]() ,
,
∵H,H′和G,G′關于BC對稱,
∴HH′⊥BC,GG′⊥BC,
∴在RT△BHI中,BI=![]() BH=
BH=![]() ,HI=
,HI=![]() BH=
BH=![]()
![]() ,
,
在RT△CGJ中,CJ=![]() CG=
CG=![]() ,GJ=
,GJ=![]() CG=
CG=![]()
![]() ,
,
∴HH′=2HI=![]() ,GG′=2GJ=
,GG′=2GJ=![]() x,IJ=4-
x,IJ=4-![]() -
-![]() ,
,
∴y=![]() (
(![]() +
+![]() x)(4-
x)(4-![]() -
-![]() )(1≤x≤4),
)(1≤x≤4),
②由①得,y=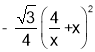 +2
+2![]() (
(![]() +x),
+x),
設![]() +x=a,得y=-
+x=a,得y=-![]() a2+2
a2+2![]() a,
a,
當a=4時,y最大=4![]() ,
,
此時![]() +x=4,解得x=2.
+x=4,解得x=2.


科目:初中數學 來源: 題型:
【題目】如圖,有一條兩岸平行的河流,一數學實踐活動小組在無法涉水過河情況下,成功測得河的寬度,他們的做法如下:
①正對河流對岸的一顆樹A,在河的一岸選定一點B;
②沿河岸直走15步恰好到達一樹C處,繼續前行15步到達D處;
③自D處沿河岸垂直的方向行走,當到達A樹正好被C樹遮擋住的E處時,停止行走;
④測得DE的長就是河寬.
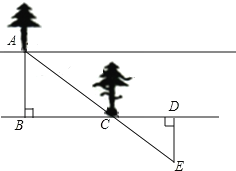
請你運用所學知識說明他們做法是正確的.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設函數![]() (其中k為常數).
(其中k為常數).
(1)當k=-2時,函數y存在最值嗎?若存在,請求出這個最值;
(2)在x>0時,要使函數y的的值隨x的增大而減小,求k應滿足的條件;
(3)若函數y的圖象與x軸交于A、B兩點,與y軸交于點C,求能使△ABC為等腰三角形的k的值.(分母保留根號,不必化簡)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖,直角三角形的頂點A、B在x軸上,ABC=90 ,BC//y軸,且C點在第二象限,B點為(-3,0),將直角三角形ABC沿x軸水平向右平移m個單位,得到對應的直角三角形DEF,其中點A、B、C分別對應點D、E、F,求:
(1)用含m的式子表示E點坐標及AD的長度;
(2)若C點為(-3,n),設四邊形BEFC的周長為y,試用含m、n的式子表示周長y;
(3)在(2)的條件下,點P和點Q分別以1個單位/秒,2個單位/秒的速度同時從B點出發,其中,P點沿B→C→F→E→B的方向運動,Q點沿B→E→F→C→B的方向運動,相遇時則停止運動。當P點到達C點時,Q點恰到達E點;從B點出發起,6秒后P點與Q點相遇停止了運動,求四邊形ADFC的面積。

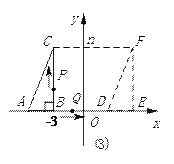
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解我縣2019年八年級末數學學科成績,從中抽取200名八年級學生期末數學成績進行統計分析,在這個問題中,樣本是指( )
A.200
B.我縣2019年八年級學生期末數學成績
C.被抽取的200名八年級學生
D.被抽取的200名我縣八年級學生期末數學成績
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com