
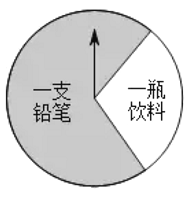
【題目】某商場有一個可以自由轉動的圓形轉盤(如圖).規定:顧客購物![]() 元以上可以獲得一次轉動轉 盤的機會,當轉盤停止時指針落在哪一個區域就獲得相應的獎品 (指針指向兩個扇形的交線時,當作指向右邊的扇形),下表是活動進行中的一組統計數據:
元以上可以獲得一次轉動轉 盤的機會,當轉盤停止時指針落在哪一個區域就獲得相應的獎品 (指針指向兩個扇形的交線時,當作指向右邊的扇形),下表是活動進行中的一組統計數據:
轉動轉盤的次數 |
|
|
|
|
|
|
落在“鉛筆"的次數 |
|
|
|
|
|
|
落在“鉛筆"的頻率 |
|
|
|
|
|
|
(1)轉動該轉盤一次,獲得鉛筆的概率約為____ ;( 結果保留小數點后一位數字);
(2)鉛筆每只![]() 元,飲料每瓶
元,飲料每瓶![]() 元,經統計該商場每天約有
元,經統計該商場每天約有![]() 名顧各參加抽獎活動,請計算該商場每天需要支出的獎品費用;
名顧各參加抽獎活動,請計算該商場每天需要支出的獎品費用;
(3)在(2)的條件下,該商場想把每天支出的獎品費用控制在![]() 元左右,則轉盤上“一瓶飲料”區域的圓心角應調整為 度.
元左右,則轉盤上“一瓶飲料”區域的圓心角應調整為 度.
【答案】(1)0.7;(2)該商場每天大致需要支出![]() 元獎品費用:(3)36
元獎品費用:(3)36
【解析】
(1)利用頻率估計概率即可求解;
(2)根據扇形統計圖,結合獲得鉛筆的概率為0.7,求出獲得一瓶飲料的概率為0.3,列出算式40000×0.7×0.5+40000×0.3×3,計算即可求解;
(3)設轉盤上“一瓶飲料”區域的圓心角應調整為n°,則![]() ,解方程即可.
,解方程即可.
解:(1)轉動該轉盤一次,獲得鉛筆的概率約為0.7;
(2)1-0.7=0.3,40000×0.7×0.5+40000×0.3×3=14000+36000=50000元;
(3)設轉盤上“一瓶飲料”區域的圓心角應調整為n°,
則![]() ,
,
解方程得:n=36.


科目:初中數學 來源: 題型:
【題目】解不等式組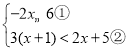 請結合題意填空,完成本題的解答.
請結合題意填空,完成本題的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的階級在數軸上表示出來;
(Ⅳ)原不等式組的解集為
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(
兩點(![]() 點位于
點位于![]() 點左側),與
點左側),與![]() 軸交于
軸交于![]() 點,連接
點,連接![]() .點
.點![]() 為拋物線的頂點,點
為拋物線的頂點,點![]() 為
為![]() .
.

(1)點![]() 是第四象限內拋物線上的一點,過點
是第四象限內拋物線上的一點,過點![]() 作
作![]() 軸交拋物線于點
軸交拋物線于點![]() ,作
,作![]() 軸于點
軸于點![]() ,作
,作![]() 軸于點
軸于點![]() ,點
,點![]() 在點
在點![]() 右邊.點
右邊.點![]() 是直線
是直線![]() 上一個動點,點
上一個動點,點![]() 是直線
是直線![]() 上一個動點,當四邊形
上一個動點,當四邊形![]() 的周長最大時,求
的周長最大時,求![]() 的最小值;
的最小值;
(2)如圖2,將原拋物線繞其對稱軸與![]() 軸的交點
軸的交點![]() 旋轉
旋轉![]() 得新的拋物線
得新的拋物線![]() ,點
,點![]() ,
,![]() 的對應點分別記為
的對應點分別記為![]() ,
,![]() ,把拋物線
,把拋物線![]() 沿直線
沿直線![]() 平移,
平移,![]() ,
,![]() 的對應點分別記為
的對應點分別記為![]() ,
,![]() 是否存在點
是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為腰的等腰三角形?若存在,請直接寫出
為腰的等腰三角形?若存在,請直接寫出![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
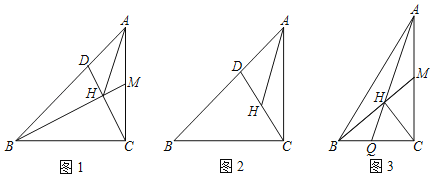
【題目】如圖,在Rt△ABC中,![]() =n,M為BC上的一點,連接BM.
=n,M為BC上的一點,連接BM.
(1)如圖1,若n=1,
①當M為AC的中點,當BM⊥CD于H,連接AH,求∠AHD的度數;
②如圖2,當H為CD的中點,∠AHD=45°,求![]() 的值和∠CAH的度數;
的值和∠CAH的度數;
(2)如圖3,CH⊥AM于H,連接CH并延長交AC于Q,M為AC中點,直接寫出tan∠BHQ的值(用含n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=![]() x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P時直線AC下方拋物線上的動點.
x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P時直線AC下方拋物線上的動點.

(1)求拋物線的解析式;(2)過點P且與y軸平行的直線l與直線AB、AC分別交于點E、F,當四邊形AECP的面積最大時,求點P的坐標;
(3)當點P為拋物線的頂點時,在直線AC上是否存在點Q,使得以C、P、Q為頂點的三角形與△ABC相似,若存在,求出點Q的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABDE是平行四邊形,C為邊B D延長線上一點,連結AC、CE,使AB=AC.
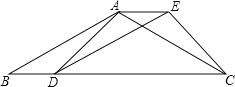
(1)求證:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四邊形ABDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在直角坐標系中
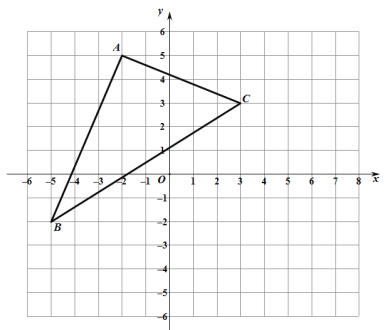
(1)請寫出△ABC各點的坐標;
(2)求出△ABC的面積;
(3)如圖,將三角形ABC向右平移3個單位長度,再向下平移2個單位長度,得到對應的三角形A1B1C1,并寫出點A1、B1、C1的坐標
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com