
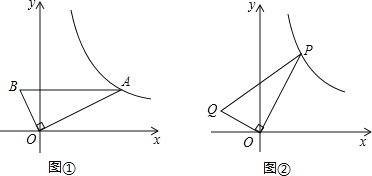
【題目】如圖①,直角三角形AOB中,∠AOB=90°,AB平行于x軸,OA=2OB,AB=5,反比例函數的圖象經過點A.
(1)直接寫出反比例函數的解析式;
(2)如圖②,P(x,y)在(1)中的反比例函數圖象上,其中1<x<8,連接OP,過O 作OQ⊥OP,且OP=2OQ,連接PQ.設Q坐標為(m,n),其中m<0,n>0,求n與m的函數解析式,并直接寫出自變量m的取值范圍;
(3)在(2)的條件下,若Q坐標為(m,1),求△POQ的面積.
【答案】(1)y=![]() ;(2)n=
;(2)n=![]() (﹣4<m<﹣
(﹣4<m<﹣![]() );(3)5.
);(3)5.
【解析】
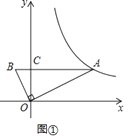
(1)如圖①,
∵∠AOB=90°,
∴OA2+OB2=AB2,
∵OA=2OB,AB=5,
∴4OB2+OB2=25,解得OB=![]() ,
,
∴OA=2![]() ,
,
∵AB平行于x軸,
∴OC⊥AB,
∴![]() OCAB=
OCAB=![]() OBOA,即OC=
OBOA,即OC=![]() =2,
=2,
在Rt△AOC中,AC=4,
∴A點坐標為(4,2),
設過A點的反比例函數解析式為y=![]() ,
,
∴k=4×2=8,
∴反比例函數解析式為y=![]() ;
;
(2)分別過P、Q作x軸垂線,垂足分別為D、H,如圖②,
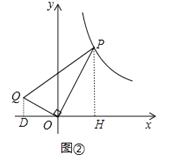
∵OQ⊥OP,
∴∠POH+∠QOD=90°,
∵∠POH+∠OPH=90°,
∴∠QOD=∠OPH,
∴Rt△POH∽Rt△OQD,
∴![]() ,
,
∵P(x,y)在(1)中的反比例函數圖象上,其中1<x<8,Q點坐標為(m,n),其中m<0,n>0,OP=2OQ,
∴PH=y,OH=x,OD=﹣m,QD=n,
∴![]() ,解得x=2n,y=﹣2m,
,解得x=2n,y=﹣2m,
∵y=![]() ,
,
∴2n(﹣2m)=8,
∴mn=﹣2(﹣4<m<﹣![]() ),
),
∴n=![]() (﹣4<m<﹣
(﹣4<m<﹣![]() );
);
(3)∵n=1時,m=﹣2,即Q點坐標為(﹣2,1),
∴OQ=![]() ,
,
∴OP=2OQ=![]() ,
,
∴S△POQ=![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作⊙O交BC于點D,過點D作AC的垂線交AC于點E,交AB的延長線于點F.
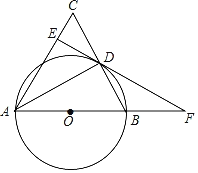
(1)求證:DE與⊙O相切;
(2)若CD=BF,AE=3,求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某個體商戶購進某種電子產品的進價是50元/個,根據市場調研發現售價是80元/個時,每周可賣出160個.若銷售單價每個降低2元,則每周可多賣出![]() 個.設銷售價格每個降低
個.設銷售價格每個降低![]() 元,每周銷售量為y個.
元,每周銷售量為y個.
(1)求出銷售量![]() 個與降價
個與降價![]() 元之間的函數關系式;
元之間的函數關系式;
(2)設商戶每周獲得的利潤為W元,當銷售單價定為多少元時,每周銷售利潤最大,最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
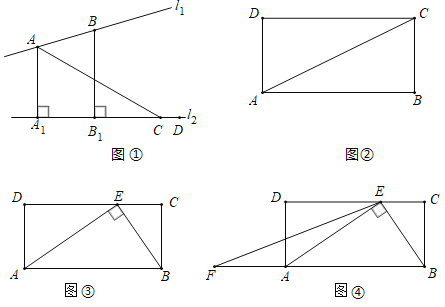
【題目】如圖①,平面內的兩條直線![]() 點
點![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 上,過
上,過![]() 兩點分別作
兩點分別作![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,我們把線段
,我們把線段![]() 叫做線段
叫做線段![]() 在直線
在直線![]() 上的正投影,其長度可記為
上的正投影,其長度可記為![]() 或
或![]() 特別地,線段
特別地,線段![]() 在直線
在直線![]() 上的正投影就是線段
上的正投影就是線段![]() .請依據上述定義解決如下問題:
.請依據上述定義解決如下問題:
(1)如圖①,若![]() ,則
,則![]() .
.
(2)如圖②,在矩形![]() 中,
中,![]() ,
,![]() ,則
,則![]() .
.
(3)如圖③,在矩形![]() 中,點
中,點![]() 在
在![]() 邊上(
邊上(![]() ),連接
),連接![]() 、
、![]() ,
,![]()
①若![]() ,求矩形
,求矩形![]() 的面積.
的面積.
②如圖④,點![]() 在
在![]() 延長線上,連按
延長線上,連按![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
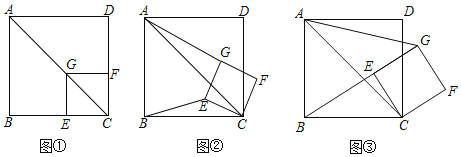
【題目】如圖(1),將正方形ABCD與正方形GECF的頂點C重合,當正方形GECF的頂點G在正方形ABCD的對角線AC上時,![]() 的值為______.
的值為______.
如圖(2),將正方形CEGF繞點C順時針方向旋轉a角(0°<a<45°),猜測AG與BE之間的數量關系,并說明理由.
如圖(3),將正方形CEGF繞點C順時針方向旋轉a角(45°<a<90°)使得B、E、G三點在一條直線上,此時tan∠GAC=![]() ,AG=6,求△BCE的面積.
,AG=6,求△BCE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】石獅泰禾某童裝專賣店在銷售中發現,一款童裝每件進價為80元,銷售價為120元時,每天可售出20件,為了迎接“十一”國慶節,商店決定采取適當的降價措施,以擴大銷售量,增加利潤,經市場調查發現,如果每件童裝降價1元,那么平均可多售出2件.
(1)設每件童裝降價x元時,每天可銷售______ 件,每件盈利______ 元;(用x的代數式表示)
(2)每件童裝降價多少元時,平均每天贏利1200元.
(3)要想平均每天贏利2000元,可能嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與
與![]() 軸、
軸、![]() 軸分別相交于點A(-1,0)和B(0,3),其頂點為D。
軸分別相交于點A(-1,0)和B(0,3),其頂點為D。
(1)求這條拋物線的解析式;
(2)畫出此拋物線;
(3)若拋物線與![]() 軸的另一個交點為E,求△ODE的面積;
軸的另一個交點為E,求△ODE的面積;
(4)拋物線的對稱軸上是否存在點P使得△PAB的周長最短。若存在請求出點P的坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
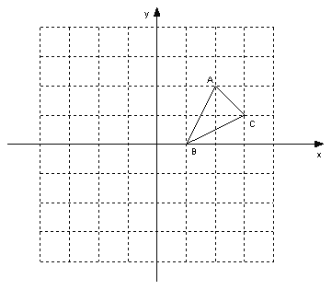
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點B的坐標為(1,0)
(1)畫出△ABC關于x軸對稱的△A1B1C1,
(2)畫出將△ABC繞原點O按逆時針旋轉90°所得的△A2B2C2,
(3)△A1B1C1與△A2B2C2成軸對稱圖形嗎?若成軸對稱圖形,畫出所有的對稱軸并寫出對稱軸;
(4)△A1B1C1與△A2B2C2成中心對稱圖形嗎?若成中心對稱圖形,寫出所有的對稱中心的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學在一次數學測驗中解答的填空題,其中答對的是( )
A.若![]() ,則x=2B.若
,則x=2B.若![]() 的一個根是1,則k=2
的一個根是1,則k=2
C.若![]() ,則x=2D.若
,則x=2D.若![]() 的值為0,則x=1或2
的值為0,則x=1或2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com