
如圖,在平面直角坐標系中,拋物線y=ax2+bx+6經過點A(-3,0)和點B(2,0).直線y=h(h為常數,且0<h<6)與BC交于點D,與y軸交于點E,與AC交于點F,與拋物線在第二象限交于點G.
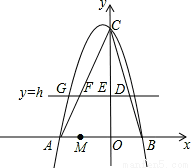
(1)求拋物線的解析式;
(2)連接BE,求h為何值時,△BDE的面積最大;
(3)已知一定點M(-2,0).問:是否存在這樣的直線y=h,使△OMF是等腰三角形?若存在,請求出h的值和點G的坐標;若不存在,請說明理由.
(1) y=-x2-x+6.(2) 當h=3時,△BDE的面積最大,最大面積是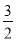 .(3) 存在這樣的直線y=2或y=4,使△OMF是等腰三角形,當h=4時,點G的坐標為(-2,4);當h=2時,點G的坐標為(
.(3) 存在這樣的直線y=2或y=4,使△OMF是等腰三角形,當h=4時,點G的坐標為(-2,4);當h=2時,點G的坐標為(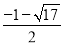 ,2).
,2).
【解析】
試題分析:(1)由拋物線y=ax2+bx+6經過點A(-3,0)和點B(2,0),利用待定系數法即可求得拋物線的解析式;
(2)首先利用待定系數法求得經過點B和點C的直線的解析式,由題意可得點E的坐標為(0,h),則可求得點D的坐標為(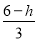 ,h),則可得S△BDE=
,h),則可得S△BDE=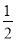 •OE•DE=
•OE•DE=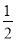 •h•
•h•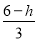
=- (h-3)2+
(h-3)2+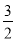 ,然后由二次函數的性質,即可求得△BDE的面積最大;
,然后由二次函數的性質,即可求得△BDE的面積最大;
(3)分別從①若OF=OM,則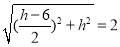 、②若OF=MF,則
、②若OF=MF,則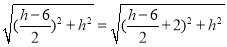 與③若MF=OM,則
與③若MF=OM,則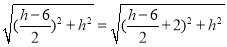 去分析求解即可求得答案.
去分析求解即可求得答案.
試題解析:(1)∵拋物線y=ax2+bx+6經過點A(-3,0)和點B(2,0),
∴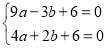 .
.
解得: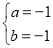 .
.
∴拋物線的解析式為y=-x2-x+6.
(2)∵把x=0代入y=-x2-x+6,得y=6.
∴點C的坐標為(0,6).
設經過點B和點C的直線的解析式為y=mx+n,則
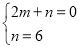 ,
,
解得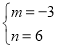 .
.
∴經過點B和點C的直線的解析式為:y=-3x+6.
∵點E在直線y=h上,
∴點E的坐標為(0,h).
∴OE=h.
∵點D在直線y=h上,
∴點D的縱坐標為h.
把y=h代入y=-3x+6,得h=-3x+6.
解得x=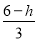 .
.
∴點D的坐標為(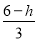 ,h).
,h).
∴DE=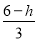 .
.
∴S△BDE=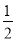 •OE•DE=
•OE•DE=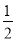 •h•
•h•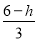
=-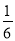 (h-3)2+
(h-3)2+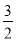 .
.
∵-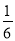 <0且0<h<6,
<0且0<h<6,
∴當h=3時,△BDE的面積最大,最大面積是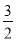 .
.
(3)存在符合題意的直線y=h.
設經過點A和點C的直線的解析式為y=kx+p,則
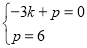 ,
,
解得
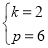 .
.
故經過點A和點C的直線的解析式為y=2x+6.
把y=h代入y=2x+6,得h=2x+6.
解得x=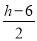 .
.
∴點F的坐標為(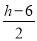 ,h).
,h).
在△OFM中,OM=2,OF=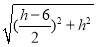 ,MF=
,MF=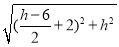 .
.
①若OF=OM,則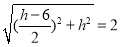 ,
,
整理,得5h2-12h+20=0.
∵△=(-12)2-4×5×20=-256<0,
∴此方程無解.
∴OF=OM不成立.
②若OF=MF,則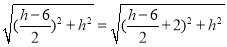 ,
,
解得h=4.
把y=h=4代入y=-x2-x+6,得-x2-x+6=4,
解得x1=-2,x2=1.
∵點G在第二象限,
∴點G的坐標為(-2,4).
③若MF=OM,則 ,
,
解得h1=2,h2=-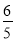 (不合題意,舍去).
(不合題意,舍去).
把y=h1=2代入y=-x2-x+6,得-x2-x+6=2.
解得x1=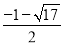 ,x2=
,x2=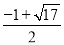 .
.
∵點G在第二象限,
∴點G的坐標為(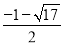 ,2).
,2).
綜上所述,存在這樣的直線y=2或y=4,使△OMF是等腰三角形,當h=4時,點G的坐標為(-2,4);當h=2時,點G的坐標為(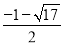 ,2).
,2).
考點:二次函數綜合題.


科目:初中數學 來源:2014-2015學年安徽省心學校九年級上學期數學試卷(解析版) 題型:解答題
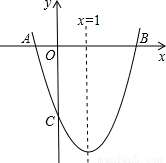
如圖,已知拋物線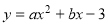 的對稱軸為直線
的對稱軸為直線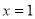 ,交
,交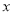 軸于A、B兩點,交
軸于A、B兩點,交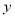 軸于C點,其中B點的坐標為(3,0)。
軸于C點,其中B點的坐標為(3,0)。
(1)直接寫出A點的坐標;
(2)求二次函數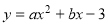 的解析式。
的解析式。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省七年級上學期期中檢測數學試卷(解析版) 題型:選擇題
若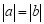 ,則a與b的關系是( )
,則a與b的關系是( )
A.a=b B.a=b C.a=b=0 D.a=b或a=-b
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川中江縣繼光實驗學校九年級上期末模擬考試數學試卷(解析版) 題型:選擇題
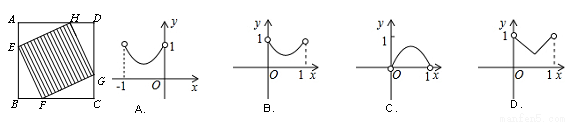
如圖,正方形ABCD的邊長為1,E、F、G、H分別為各邊上的點,且AE=BF=CG=DH,設小正方形EFGH的面積為s,AE為x,則s關于x的函數圖象大致是 ( )
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川中江縣繼光實驗學校九年級上期末模擬考試數學試卷(解析版) 題型:選擇題
在一個不透明的塑料袋中裝有紅色、白色球共40,除顏色外其它都相同,小明通過多次摸球試驗后發現,其中摸到紅色球的頻率穩定在15%左右,則口袋中紅色球可能有( )
A.4個 B.6個 C.34個 D.36個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省自貢市九年級上學期期末統一考試數學試卷(解析版) 題型:解答題
如圖,AB為⊙O的直徑,PD切⊙O于點C,交AB的延長線于點D,且∠D=2∠CAD.
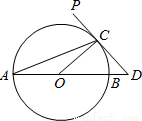
(1)求∠D的度數;
(2)若CD=1,求BD的長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省涼山州九年級上學期期末數學試卷(解析版) 題型:解答題
如圖,有一個可以自由轉動的轉盤被平均分成3個扇形,分別標有1、2、3三個數字,小王和小李各轉動一次轉盤為一次游戲,當每次轉盤停止后,指針所指扇形內的數為各自所得的數,一次游戲結束得到一組數(若指針指在分界線時重轉).
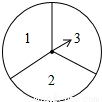
(1)請你用樹狀圖或列表的方法表示出每次游戲可能出現的所有結果;
(2)求每次游戲結束得到的一組數恰好是方程x2-3x+2=0的解的概率.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市九年級第二次月考數學試卷(解析版) 題型:選擇題
用配方法解方程x2﹣2x﹣1=0時,配方后得的方程為( )
A.(x+1)2=0 B.(x﹣1)2=0 C.(x+1)2=2 D.(x﹣1)2=2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com