
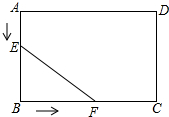
 如圖,在矩形ABCD中,AB=5cm,BC=7cm,點E從點A出發,沿AB方向以1cm/s的速度向點B移動,同時,點F從點B出發,沿BC方向以2cm/s的速度向點C移動,當點F到達點C時,兩點同時停止運動,設運動時間為t秒.
如圖,在矩形ABCD中,AB=5cm,BC=7cm,點E從點A出發,沿AB方向以1cm/s的速度向點B移動,同時,點F從點B出發,沿BC方向以2cm/s的速度向點C移動,當點F到達點C時,兩點同時停止運動,設運動時間為t秒.分析 (1)用t表示出BE及BF的長,再由三角形的面積公式即可得出結論;
(2)分△BEF∽△ABD與△BEF與△ADB兩種情況進行討論即可.
解答 解:(1)∵AB=5cm,BC=7cm,點E從點A出發,沿AB方向以1cm/s的速度向點B移動,同時,點F從點B出發,沿BC方向以2cm/s的速度向點C移動,
∴BE=5-t,BF=2t.
∵△BEF的面積為5cm2,
∴$\frac{1}{2}$BF•BE=5,即$\frac{1}{2}$×2t×(5-t)=5,解得t1=$\frac{5+\sqrt{5}}{2}$(舍去),t2=$\frac{5-\sqrt{5}}{2}$.
答:當t=$\frac{5-\sqrt{5}}{2}$時,△BEF的面積為5cm2;
(2)∵BE=5-t,BF=2t,
∴當△BEF∽△ABD時,$\frac{BE}{AB}$=$\frac{BF}{AD}$,即$\frac{5-t}{5}$=$\frac{2t}{7}$,解得t=$\frac{35}{17}$;
當△BEF與△ADB時,$\frac{BE}{AD}$=$\frac{BF}{AB}$,即$\frac{5-t}{7}$=$\frac{2t}{5}$,解得t=$\frac{25}{19}$.
綜上所述,當t為$\frac{35}{17}$秒或$\frac{25}{19}$秒時,BEF與△ABD相似.
點評 本題考查的是相似三角形的判定,在解答此題時要注意進行分類討論,不要漏解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
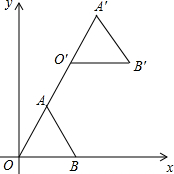 已知:如圖,在平面直角坐標系中,正三角形OAB的頂點B的坐標為(2,0),點A在第一象限內
已知:如圖,在平面直角坐標系中,正三角形OAB的頂點B的坐標為(2,0),點A在第一象限內查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com