分析:(1)連接AB,BF,得出
=
,再根據⊙O
1與⊙O
2是等圓,得出∠ABC=∠ABF,即可證出AD=AF;
(2)連接O
1B,O
2B,O
1C,O
2E,O
1O
2,BE,根據⊙O
1與⊙O
2的弧AB相等,得出∠C=∠E,BC=BE,再證出△O
1BC≌△O
2BE,得出∠O
1BC=∠O
2BE,∠CBE=∠O
1BO
2,再根據O
1O
2=
,
O
1B=O
2B=1,得出O
1O
2B為等腰直角三角形,∠CBE=∠O
1BO
2=90°,從而證出△CBE也為等腰直角三角形,即可得出CE=
BC.
解答:解:(1)連接AB,BF,
∵C從點A出發,點F從點A出發,兩點的運動速度相同,

∴
=
,
∵⊙O
1與⊙O
2是等圓,
∴∠ABC=∠ABF,
∴AD=AF;
(2)連接O
1B,O
2B,O
1C,O
2E,O
1O
2,BE,
∵⊙O
1與⊙O
2的弧AB相等,
∴∠C=∠E,
∴BC=BE,
在△O
1BC和△O
2BE中,
∴△O
1BC≌△O
2BE(SSS),
∴∠O
1BC=∠O
2BE,∠CBE=∠O
1BO
2,
∵O
1O
2=
,
O
1B=O
2B=1,
∴O
1O
2B為等腰直角三角形,
∴∠CBE=∠O
1BO
2=90°,
∴△CBE也為等腰直角三角形,
∴CE=
BC.
點評:此題考查了圓的綜合,用到的知識點是全等三角形的判定與性質、圓的有關性質、等腰三角形的判定與性質,關鍵是作出輔助線,證出△CBE也為等腰直角三角形.

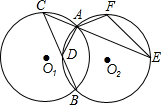 如圖,半徑為1的等圓⊙O1與⊙O2相交于A、B兩點,點C從點A出發,在⊙O1,上逆時針運動;同時點F從點A出發,在⊙O2上順時針運動,兩點的運動速度相同,⊙O1的弦CB交⊙O2于點D.
如圖,半徑為1的等圓⊙O1與⊙O2相交于A、B兩點,點C從點A出發,在⊙O1,上逆時針運動;同時點F從點A出發,在⊙O2上順時針運動,兩點的運動速度相同,⊙O1的弦CB交⊙O2于點D.






 閱讀快車系列答案
閱讀快車系列答案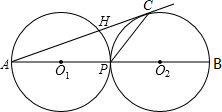 如圖,外切于P點的⊙O1和⊙O2是半徑為3cm的等圓,連心線交⊙O1于點A,交⊙O2于點B,AC與⊙O2相切于點C,連接PC,則PC的長為( )
如圖,外切于P點的⊙O1和⊙O2是半徑為3cm的等圓,連心線交⊙O1于點A,交⊙O2于點B,AC與⊙O2相切于點C,連接PC,則PC的長為( )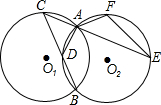 如圖,半徑為1的等圓⊙O1與⊙O2相交于A、B兩點,點C從點A出發,在⊙O1,上逆時針運動;同時點F從點A出發,在⊙O2上順時針運動,兩點的運動速度相同,⊙O1的弦CB交⊙O2于點D.
如圖,半徑為1的等圓⊙O1與⊙O2相交于A、B兩點,點C從點A出發,在⊙O1,上逆時針運動;同時點F從點A出發,在⊙O2上順時針運動,兩點的運動速度相同,⊙O1的弦CB交⊙O2于點D. ,射線CA交⊙O2于點E,試探究CE與CB之間的數量關系.
,射線CA交⊙O2于點E,試探究CE與CB之間的數量關系.