
分析 (1)先把方程化為一般式,然后利用求根公式法解方程;
(2)先把方程化為一般式,然后利用因式分解法解方程.
解答 解:(1)x2+x-8=0,
△=b2-4ac=1+32=33>0,
∴x=$\frac{-1±\sqrt{33}}{2}$,
∴x1=$\frac{-1+\sqrt{33}}{2}$,x2=$\frac{-1-\sqrt{33}}{2}$;
(2)移項得:x2-2x-35=0,
(x-7)(x+5)=0,
x-7=0或x+5=0,
所以x1=7,x2=-5.
點評 本題考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右邊化為0,再把左邊通過因式分解化為兩個一次因式的積的形式,那么這兩個因式的值就都有可能為0,這就能得到兩個一元一次方程的解,這樣也就把原方程進行了降次,把解一元二次方程轉化為解一元一次方程的問題了(數學轉化思想).也考查了公式法解一元二次方程.


科目:初中數學 來源: 題型:選擇題
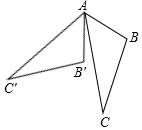 如圖所示,△ABC中,∠BAC=32°,將△ABC繞點A按順時針方向旋轉55°,對應得到△AB′C′,則∠B′AC的度數為( )
如圖所示,△ABC中,∠BAC=32°,將△ABC繞點A按順時針方向旋轉55°,對應得到△AB′C′,則∠B′AC的度數為( )| A. | 22° | B. | 23° | C. | 24° | D. | 25° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 球隊 | 比賽現場 | 勝場 | 負場 | 積分 |
| 前進 | 14 | 10 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 遠大 | 14 | 7 | 7 | 21 |
| 衛星 | 14 | 4 | 10 | 18 |
| 備注:積分=勝場積分+負場積分 | ||||
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -(2x+5)=2x+5 | B. | -$\frac{1}{2}$(4x-2)=-2x+2 | C. | -a+b=-(a-b) | D. | 2-3x=(3x+2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com