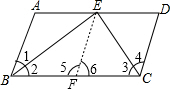
證明:在BC上取點F,使BF=BA,連接EF,
∵BE、CE分別是∠ABC和∠BCD的平分線,
∴∠1=∠2,∠3=∠4.
在△ABE和△FBE中,
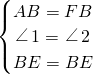
,
∴△ABE≌△FBE(SAS),
∴∠A=∠5.
∵AB∥CD,
∴∠A+∠D=180°,
∴∠5+∠D=180.
∵∠5+∠6=180°,
∴∠6=∠D.
在△CDE和△CFE中,

,
∴△CDE≌△CFE(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD.
分析:在BC上取點F,使BF=BA,連接EF,由角平分線的性質可以得出∠1=∠2,從而可以得出△ABE≌△FBE,可以得出∠A=∠5,進而可以得出△CDE≌△CFE,就可以得出CD=CF,即可得出結論.
點評:本題考查了角平分線的性質的運用,全等三角形的判定及性質的運用,解答時運用截取法正確作輔助線是關鍵.

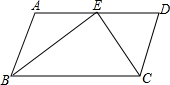 如圖,AB∥CD,BE、CE分別是∠ABC和∠BCD的平分線,點E在AD上.
如圖,AB∥CD,BE、CE分別是∠ABC和∠BCD的平分線,點E在AD上.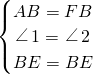 ,
,
 ,
,

 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案