
【題目】在一個不透明的盒子里裝有黑、白兩種顏色的球共50個,這些球除顏色外其余完全相同.王穎做摸球試驗,攪勻后,她從盒子里隨機摸出一個球記下顏色后,再把球放回盒子中,不斷重復上述過程,如表是試驗中的一組統計數據:
摸球的次數n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次數m | 65 | 124 | 178 | 302 | 480 | 600 | 1800 |
摸到白球的頻率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.6 | 0.6 | 0.6 |
(1)請估計:當n很大時,摸到白球的頻率將會接近 ;(精確到0.1)
(2)若從盒子里隨機摸出一個球,則摸到白球的概率的估計值為 ;
(3)試估算盒子里黑、白兩種顏色的球各有多少個?
【答案】(1)0.6;(2)0.6;(3)盒子里黑顏色的球有20只,盒子白顏色的球有30只
【解析】
(1)觀察表格找到逐漸穩定到的常數即可;
(2)概率接近于(1)得到的頻率;
(3)白球個數=球的總數×得到的白球的概率,讓球的總數減去白球的個數即為黑球的個數,問題得解.
(1)∵摸到白球的頻率約為0.6,
∴當n很大時,摸到白球的頻率將會接近0.6;
故答案為:0.6;
(2)∵摸到白球的頻率為0.6,
∴若從盒子里隨機摸出一只球,則摸到白球的概率的估計值為0.6;
(3)黑白球共有20只,
白球為:50×0.6=30(只),
黑球為:50﹣30=20(只).
答:盒子里黑顏色的球有20只,盒子白顏色的球有30只.


科目:初中數學 來源: 題型:
【題目】春節期間,支付寶“集五福”活動中的“集五福”福卡共分為5種,分別為富強福、和諧福、友善福、愛國福、敬業福,從國家、社會和個人三個層面體現了社會主義核心價值觀的價值目標.
(1)小明一家人春節期間參與了支付寶“集五福”活動,小明和姐姐都缺一個“敬業福”,恰巧爸爸有一個可以送給他們其中一個人,兩個人各設計了一個游戲,獲勝者得到“敬業福”.
在一個不透明盒子里放入標號分別為1,2,3,4的四個小球,這些小球除了標號數字外都相同,將小球搖勻.
小明的游戲規則是:從盒子中隨機摸出一個小球,摸到標號數字為奇數小球,則判小明獲勝,否則,判姐姐獲勝.請判斷,此游戲規則對小明和姐姐公平嗎?說明理由.
姐姐的游戲規則是:小明從盒子中隨機摸出一個小球,記下標號數字后放回盒里,充分搖勻后,姐姐再從盒中隨機摸出一個小球,并記下標號數字.若兩次摸到小球的標號數字同為奇數或同為偶數,則判小明獲勝,若兩次摸到小球的標號數字為一奇一偶,則判姐姐獲勝.請用列表法或畫樹狀圖的方法進行判斷此游戲規則對小明和姐姐是否公平.
(2)“五福”中體現了社會主義核心價值觀的價值目標的個人層面有哪些?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的過長是3,BP=CQ,連接AQ,DP交于點O,并分別與邊CD、BC交于點F、E,連接AE.
(1)求證:AQ⊥DP;
(2)求證:AO2=ODOP;
(3)當BP=1時,求QO的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐—探究正方形旋轉中的數學問題
問題情境:已知正方形![]() 中,點
中,點![]() 在
在![]() 邊上,且
邊上,且![]() .將正方形
.將正方形![]() 繞點
繞點![]() 順時針旋轉得到正方形
順時針旋轉得到正方形![]() (點
(點![]() ,
,![]() ,
,![]() ,
,![]() 分別是點
分別是點![]() ,
,![]() ,
,![]() ,
,![]() 的對應點).同學們通過小組合作,提出下列數學問題,請你解答.
的對應點).同學們通過小組合作,提出下列數學問題,請你解答.
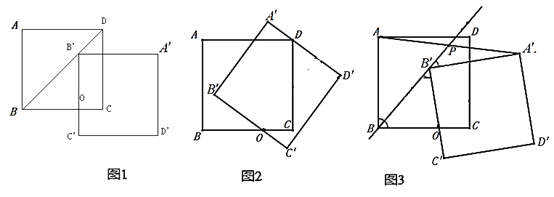
特例分析:(1)“樂思”小組提出問題:如圖1,當點![]() 落在正方形
落在正方形![]() 的對角線
的對角線![]() 上時,設線段
上時,設線段![]() 與
與![]() 交于點
交于點![]() .求證:四邊形
.求證:四邊形![]() 是矩形;
是矩形;
(2)“善學”小組提出問題:如圖2,當線段![]() 經過點
經過點![]() 時,猜想線段
時,猜想線段![]() 與
與![]() 滿足的數量關系,并說明理由;
滿足的數量關系,并說明理由;
深入探究:(3)請從下面![]() ,
,![]() 兩題中任選一題作答.我選擇題.
兩題中任選一題作答.我選擇題.
A.在圖2中連接![]() 和
和![]() ,請直接寫出
,請直接寫出![]() 的值.
的值.
B.“好問”小組提出問題:如圖3,在正方形![]() 繞點
繞點![]() 順時針旋轉的過程中,設直線
順時針旋轉的過程中,設直線![]() 交線段
交線段![]() 于點
于點![]() .連接
.連接![]() ,并過點
,并過點![]() 作
作![]() 于點
于點![]() .請在圖3中補全圖形,并直接寫出
.請在圖3中補全圖形,并直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】光污染是繼廢氣、廢水、廢渣和噪聲等污染之后的一種新的環境污染源,主要包括白亮污染、人工白晝污染和彩光污染,如圖,小明家正對面的高樓外墻上安裝著一幅巨型廣告宣傳牌AB,小明想要測量窗外的廣告宣傳牌AB的高度,他發現晚上家里熄燈后對面樓上的廣告宣傳牌從A處發出的光恰好從窗戶的最高點C處射進房間落在地板上F處,從窗戶的最低點D處射進房間向落在地板上E處(B、O、E、F在同一直線E),小明測得窗戶距地面的高度OD=1m,窗高CD=1.5m,并測得OE=1m,OF=3m.請根據以上測量數據,求廣告宣傳牌AB的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
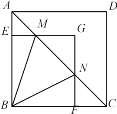
【題目】如圖,正方形ABCD邊長為3,M、N在對角線AC上且∠MBN=45°,作ME⊥AB于點E、NF⊥BC于點F,反向延長ME、NF交點G,則GEGF的值是( )
A.3B.3![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中
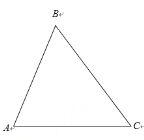
(1)請你利用無刻度的直尺和圓規在平面內畫出滿足PB2+PC2=BC2的所有點P構成的圖形,并在所作圖形上用尺規確定到邊AC、BC距離相等的點P.(作圖必須保留作圖痕跡)
(2)在(1)的條件下,連接BP,若BC=15,AC=14,AB=13,求BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
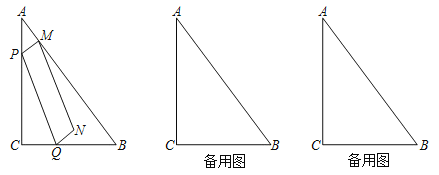
【題目】如圖,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,點P、Q分別在邊AC、射線CB上,且AP=CQ,過點P作PM⊥AB,垂足為點M,聯結PQ,以PM、PQ為鄰邊作平行四邊形PQNM,設AP=x,平行四邊形PQNM的面積為y.
(1)當平行四邊形PQNM為矩形時,求∠PQM的正切值;
(2)當點N在△ABC內,求y關于x的函數解析式,并寫出它的定義域;
(3)當過點P且平行于BC的直線經過平行四邊形PQNM一邊的中點時,直接寫出x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
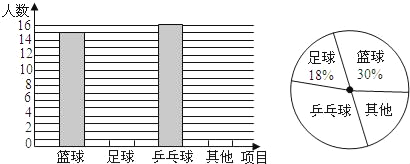
【題目】在大課間活動中,同學們積極參加體育鍛煉,小明就本班同學“我最喜愛的體育項目”進行了一次調查統計,下面是他通過收集數據后,繪制的兩幅不完整的統計圖.請你根據圖中提供的信息,解答以下問題:
(1)該班共有_____名學生;
(2)補全條形統計圖;
(3)在扇形統計圖中,“乒乓球”部分所對應的圓心角度數為_____;
(4)學校將舉辦體育節,該班將推選5位同學參加乒乓球活動,有3位男同學(A,B,C)和2位女同學(D,E),現準備從中選取兩名同學組成雙打組合,用樹狀圖或列表法求恰好選出一男一女組成混合雙打組合的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com