
【題目】在![]() 中,
中,![]() .
.
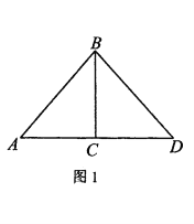
(1)如圖1,若將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() 連接
連接![]() 則
則![]() 的面積;
的面積;
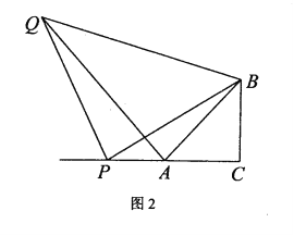
(2)如圖2,點![]() 為
為![]() 延長線上一個動點,連接
延長線上一個動點,連接![]() 以
以![]() 為直角項點,
為直角項點,![]() 為直角邊作等腰直角
為直角邊作等腰直角![]() 連接
連接![]() ,求證:
,求證:![]() ;
;
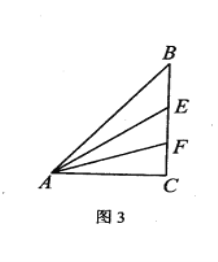
(3)如圖3,點![]() 為線段
為線段![]() 上兩點,且
上兩點,且![]() 點
點![]() 是線段
是線段![]() 上一個動點,點
上一個動點,點![]() 是線段
是線段![]() 上一個動點,是否存在點
上一個動點,是否存在點![]() 使
使![]() 的值最小,若存在,求出最小值;若不存在,說明理由.
的值最小,若存在,求出最小值;若不存在,說明理由.
科目:初中數學 來源: 題型:
【題目】(6分)如圖,菱形ABCD的對角線AC,BD相交于點O,分別延長OA,OC到點E,F,使AE=CF,依次連接B,F,D,E各點.

(1)求證:△BAE≌△BCF;
(2)若∠ABC=50°,則當∠EBA= °時,四邊形BFDE是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】工人師傅用一塊長為10dm,寬為6dm的矩形鐵皮制作一個無蓋的長方體容器,需要將四角各裁掉一個正方形.(厚度不計)

(1)在圖中畫出裁剪示意圖,用實線表示裁剪線,虛線表示折痕;并求長方體底面面積為12dm2時,裁掉的正方形邊長多大?
(2)若要求制作的長方體的底面長不大于底面寬的五倍,并將容器進行防銹處理,側面每平方分米的費用為0.5元,底面每平方分米的費用為2元,裁掉的正方形邊長多大時,總費用最低,最低為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】網絡銷售是一種重要的銷售方式.某鄉鎮農貿公司新開設了一家網店,銷售當地農產品.其中一種當地特產在網上試銷售,其成本為每千克10元.公司在試銷售期間,調查發現,每天銷售量y(kg)與銷售單價x(元)滿足如圖所示的函數關系(其中![]() ).
).
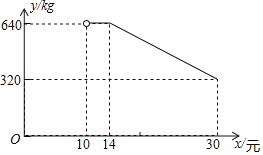
(1)直接寫出y與x之間的函數關系式及自變量的取值范圍.
(2)若農貿公司每天銷售該特產的利潤要達到3100元,則銷售單價x應定為多少元?
(3)設每天銷售該特產的利潤為W元,若![]() ,求:銷售單價x為多少元時,每天的銷售利潤最大?最大利潤是多少元?
,求:銷售單價x為多少元時,每天的銷售利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出如下定義:對于⊙O的弦MN和⊙O外一點P(M,O,N三點不共線,且點P,O在直線MN的異側),當∠MPN+∠MON=180°時,則稱點P是線段MN關于點O的關聯點.圖1是點P為線段MN關于點O的關聯點的示意圖.
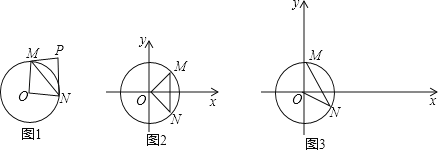
在平面直角坐標系xOy中,⊙O的半徑為1.
(1)如圖2,已知M(![]() ,
,![]() ),N(
),N(![]() ,﹣
,﹣![]() ),在A(1,0),B(1,1),C(
),在A(1,0),B(1,1),C(![]() ,0)三點中,是線段MN關于點O的關聯點的是 ;
,0)三點中,是線段MN關于點O的關聯點的是 ;
(2)如圖3,M(0,1),N(![]() ,﹣
,﹣![]() ),點D是線段MN關于點O的關聯點.
),點D是線段MN關于點O的關聯點.
①∠MDN的大小為 ;
②在第一象限內有一點E(![]() m,m),點E是線段MN關于點O的關聯點,判斷△MNE的形狀,并直接寫出點E的坐標;
m,m),點E是線段MN關于點O的關聯點,判斷△MNE的形狀,并直接寫出點E的坐標;
③點F在直線y=﹣![]() x+2上,當∠MFN≥∠MDN時,求點F的橫坐標x的取值范圍.
x+2上,當∠MFN≥∠MDN時,求點F的橫坐標x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小星同學設計的“過直線外一點作已知直線的平行線”的尺規作圖過程:

已知:如圖,直線![]() 和直線
和直線![]() 外一點
外一點![]() 求作:直線
求作:直線![]() ,使得
,使得![]()
作法:如圖
①在直線![]() 上任取一點
上任取一點![]() ,以點
,以點![]() 為圓心,
為圓心,![]() 為半徑畫圓,與直線
為半徑畫圓,與直線![]() 交于點
交于點![]() ,
,![]() 兩點
兩點
②連接![]() ,
,![]() ,延長
,延長![]() 交
交![]() 于點
于點![]()
③作![]() 的平分線
的平分線![]() ,并反向延長
,并反向延長
所以直線![]() 就是所求做的直線
就是所求做的直線
根據小星同學設計的尺規作圖過程,
(1)使用直尺和圓規,保全圖形(保留作圖痕跡)
(2)完成下面的證明
證明:![]() ,
,
![]() (_______________________)(填推理的依據)
(_______________________)(填推理的依據)
![]() 是
是![]() 的外角
的外角
![]() .
.
![]() 平分
平分![]() __________________
__________________
![]() (____________________)(填推理的依據)
(____________________)(填推理的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
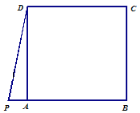
【題目】如圖,正方形 ABCD 中,P 是 BA 延長線上一點,且PDA (0 45).點 A,點 E 關于 DP 對稱,連接 ED,EP ,并延長 EP 交射線CB 于點 F ,連接 DF .
(1)請按照題目要求補全圖形.
(2)求證:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)過 P 做PH⊥DP交 DF 于點 H ,連接 BH , 猜想 AP 與 BH 的數量關系并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
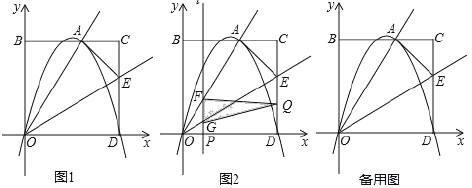
【題目】如圖1,矩形OBCD的邊OD,OB分別在x軸和y軸上,且B (0,8),D(10,0).點E是DC邊上一點,將矩形OBCD沿過點O的射線OE折疊,使點D恰好落在BC邊上的點A處.
(1)若拋物線y=ax2+bx經過點A,D,求此拋物線的解析式;
(2)若點M是(2)中拋物線對稱軸上的一點,是否存在點M,使△AME為等腰三角形?若存在,直接寫出點M的坐標;若不存在,說明理由;
(3)如圖2,動點P從點O出發沿x軸正方向以每秒1個單位的速度向終點D運動,動點Q從點D出發沿折線D﹣C﹣A以同樣的速度運動,兩點同時出發,當一點運動到終點時,另一點也隨之停止,過動點P作直線1⊥x軸,依次交射線OA,OE于點F,G,設運動時間為t(秒),△QFG的面積為S,求S與t的函數關系式,并直接寫出t的取值范圍.(t的取值應保證△QFG的存在)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() ,點
,點![]() 是射線
是射線![]() 上一動點(不與
上一動點(不與![]() 點重合),過點
點重合),過點![]() 作直線
作直線![]() 的平行線交
的平行線交![]() 軸于
軸于![]() ,過點
,過點![]() 作
作![]() 軸的垂線交直線
軸的垂線交直線![]() 于
于![]() ,連結
,連結![]() ,
,![]() ,
,![]() .
.
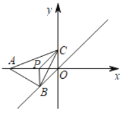
(1)當點![]() 在線段
在線段![]() 上且
上且![]() 時,
時,![]() __________.
__________.
(2)當![]() 與
與![]() 相似時,
相似時,![]() 點的橫坐標為____________.
點的橫坐標為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com