
【題目】如圖,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB邊上的中點,點D,E分別在AC,BC邊上運動,且保持AD=CE.連接DE,DF,EF.在此運動變化的過程中,下列結論: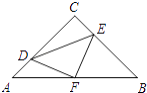
①△DFE是等腰直角三角形;
②四邊形CDFE不可能為正方形,
③DE長度的最小值為4;
④四邊形CDFE的面積保持不變;
⑤△CDE面積的最大值為8.
其中正確的結論是( )
A.①②③
B.①④⑤
C.①③④
D.③④⑤
【答案】B
【解析】解:連接CF;
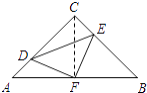
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF(SAS);
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形(故①正確).
當D、E分別為AC、BC中點時,四邊形CDFE是正方形(故②錯誤).
∵△ADF≌△CEF,
∴S△CEF=S△ADF
∴S四邊形CEFD=S△AFC,(故④正確).
由于△DEF是等腰直角三角形,因此當DE最小時,DF也最小;
即當DF⊥AC時,DE最小,此時DF= ![]() BC=4.
BC=4.
∴DE= ![]() DF=4
DF=4 ![]() (故③錯誤).
(故③錯誤).
當△CDE面積最大時,由④知,此時△DEF的面積最小.
此時S△CDE=S四邊形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8(故⑤正確).
故B符合題意.
故答案為:B.
連接CF.先證明△ADF≌△CEF可得EF=DF、∠CFE=∠AFD,再由∠AFD+∠CFD=90°可得∠EFD=90°,從而判斷①;
當D、E分別為AC、BC中點時,四邊形CDFE是正方形,從而判斷②;
由于△DEF是等腰直角三角形,因此當DE最小時,DF也最小,即當DF⊥AC時,DE最小,從而求出DF的值,進而可得DE的值,可判斷③;
由△ADF≌△CEF可得S四邊形CEFD=S△AFC,從而判斷④;
由④知,此時△DEF的面積最小.此時S△CDE=S四邊形CEFD﹣S△DEF=S△AFC﹣S△DEF,從而求出△CDE的面積,可判斷⑤.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】已知:線段![]() 、
、![]() 、
、![]() ;
;
求作:△ABC,使![]() ,
, ![]() ,
, ![]() ;
;

【答案】答案見解析
【解析】試題分析:先畫出與![]() 相等的角,再畫出
相等的角,再畫出![]() 的長,連接
的長,連接![]() ,則
,則![]() 即為所求三角形.
即為所求三角形.
試題解析:如圖所示:①先畫射線BC,
②以α的頂點為圓心,任意長為半徑畫弧,分別交α的兩邊交于為A′,C′;
③以相同長度為半徑,B為圓心,畫弧,交BC于點F,以F為圓心,C′A′為半徑畫弧,交于點E;
④在BF上取點C,使CB=a,以B為圓心,c為半徑畫圓交BE的延長線于點A,連接AC,
結論:△ABC即為所求三角形.

【題型】解答題
【結束】
15
【題目】已知:線段![]() ,
, ![]() ,求作:
,求作: ![]() ,使
,使![]() ,
, ![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一段拋物線:y=﹣x(x﹣2)(0≤x≤2)記為C1 , 它與x軸交于兩點O,A1;將C1繞A1旋轉180°得到C2 , 交x軸于A2;將C2繞A2旋轉180°得到C3 , 交x軸于A3;…如此進行下去,直至得到C2017 . 若點P是第2016段拋物線的頂點,則P點的坐標為 . 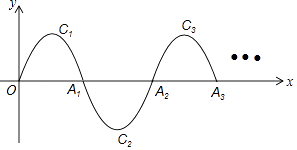
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正△ABC的邊長為2,以BC邊上的高AB1為邊作正△AB1C1,△ABC與△AB1C1公共部分的面積記為S1;再以正△AB1C1邊B1C1上的高AB2為邊作正△AB2C2,△AB1C1與△AB2C2公共部分的面積記為S2;…,以此類推,則Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家商店要進行裝修,若請甲、乙兩個裝修組同時施工,8天可以完成,需付兩組費用共3520元;若先請甲組單獨做6天,再請乙組單獨做12天可完成,需付兩組費用共3480元,問:
(1)甲、乙兩組工作一天,商店應各付多少元?
(2)已知甲組單獨做需12天完成,乙組單獨做需24天完成,單獨請哪組,商店所付費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在初三綜合素質評定結束后,為了了解年級的評定情況,現對初三某班的學生進行了評定等級的調查,繪制了如下男女生等級情況折線統計圖和全班等級情況扇形統計圖. 
(1)調查發現評定等級為合格的男生有2人,女生有1人,則全班共有名學生.
(2)補全女生等級評定的折線統計圖.
(3)根據調查情況,該班班主任從評定等級為合格和A的學生中各選1名學生進行交流,請用樹形圖或表格求出剛好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,點 D,E 分別在邊 AC,AB 上,BD 與 CE 交于點 O,給出下列三個條件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三個條件中,由哪兩個條件可以判定△ABC 是等腰三角形?(用序號寫出所有成立的情形)
(2)請選擇(1)中的一種情形,寫出證明過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC的邊OA在數軸上,O為原點,長方形OABC的面積為12,OC邊長為3.
(1)寫出數軸上點A表示的數;
(2)將長方形OABC沿數軸向右水平移動,移動后的長方形記為![]() ,若移動后的長方形
,若移動后的長方形![]() 與原長方形OABC重疊部分的面積恰好等于原長方形OABC面積的
與原長方形OABC重疊部分的面積恰好等于原長方形OABC面積的![]() 時,寫出數軸上點
時,寫出數軸上點![]() 表示的數;
表示的數;

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com