
熱氣球的探測器顯示,從熱氣球看一棟高樓頂部的仰角為30°,看這棟高樓底部的俯角為60°,熱氣球與高樓的水平距離為66 m,這棟高樓有多高(結果精確到0.1 m,參考數據:![]() ≈1.73)?
≈1.73)?
|
分析:把這個問題抽象成一個數學問題,在△ABC中,由已知可得∠B=60°,∠C=30°,過點A作AD⊥BC于點D,則AD=66 m,利用三角函數的有關知識,可以在 Rt△ABD和Rt△ACD中分別求出BD、CD的長,從而求出BC的長,即樓房的高度. 答:這棟樓高約為152.2 m. 解:如圖,過點A作AD⊥BC,垂足為點D.
根據題意,可得∠BAD=30°,∠CAD=60°,AD=66. 在Rt△ADB中,由tan∠BAD= 得BD=AD·tan∠BAD=66×tan30°=66× 在Rt△ADC中,由tan∠CAD= 得CD=AD·tan∠CAD=66×tan60°=66 所以BC=BD+CD=22 點評:當一個三角形中出現30°、45°、60°角的時候,要求一些線段的長,通常是通過作高構造直角三角形,將這些特殊角放入直角三角形中,利用直角三角形邊角關系求出線段的長. |


科目:初中數學 來源: 題型:
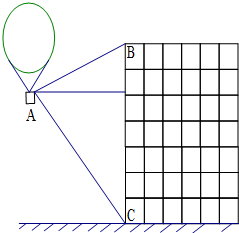 21、熱氣球的探測器顯示,從熱氣球上看一棟高樓頂部的仰角為28°,看這棟高樓底部的俯角為62°,熱氣球與高樓之間的水平距離為66m,這棟高樓有多高?(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
21、熱氣球的探測器顯示,從熱氣球上看一棟高樓頂部的仰角為28°,看這棟高樓底部的俯角為62°,熱氣球與高樓之間的水平距離為66m,這棟高樓有多高?(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)查看答案和解析>>
科目:初中數學 來源: 題型:
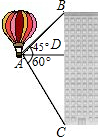 如圖,熱氣球的探測器顯示,從熱氣球看一棟高樓的頂部B的仰角為45°,看這棟高樓底部C的俯角為60°,熱氣球與高樓的水平距離AD為50m,求這棟樓的高度.(
如圖,熱氣球的探測器顯示,從熱氣球看一棟高樓的頂部B的仰角為45°,看這棟高樓底部C的俯角為60°,熱氣球與高樓的水平距離AD為50m,求這棟樓的高度.(| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
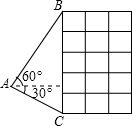 如圖熱氣球的探測器顯示,從熱氣球上看一棟高樓頂部的仰角為60°,看這棟高樓底部的俯角為30°,若熱氣球與高樓水平距離為60m,則這棟樓的高度為
如圖熱氣球的探測器顯示,從熱氣球上看一棟高樓頂部的仰角為60°,看這棟高樓底部的俯角為30°,若熱氣球與高樓水平距離為60m,則這棟樓的高度為| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•德陽)如圖,熱氣球的探測器顯示,從熱氣球A看一棟高樓頂部B的仰角為30°,看這棟高樓底部C的俯角為60°,熱氣球A與高樓的水平距離為120m,這棟高樓BC的高度為( )
(2013•德陽)如圖,熱氣球的探測器顯示,從熱氣球A看一棟高樓頂部B的仰角為30°,看這棟高樓底部C的俯角為60°,熱氣球A與高樓的水平距離為120m,這棟高樓BC的高度為( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com