
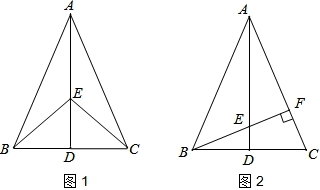
如圖1,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.
(1)求證:BE=CE;
(2)如圖2,若BE的延長線交AC于點F,且BF⊥AC,垂足為F,∠BAC=45°,原題設其它條件不變.求證:△AEF≌△BCF.
【考點】全等三角形的判定與性質;等腰三角形的性質.
【專題】證明題.
【分析】(1)根據等腰三角形三線合一的性質可得∠BAE=∠EAC,然后利用“邊角邊”證明△ABE和△ACE全等,再根據全等三角形對應邊相等證明即可;
(2)先判定△ABF為等腰直角三角形,再根據等腰直角三角形的兩直角邊相等可得AF=BF,再根據同角的余角相等求出∠EAF=∠CBF,然后利用“角邊角”證明△AEF和△BCF全等即可.
【解答】證明:(1)∵AB=AC,D是BC的中點,
∴∠BAE=∠EAC,
在△ABE和△ACE中,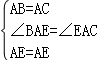 ,
,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵∠BAC=45°,BF⊥AF,
∴△ABF為等腰直角三角形,
∴AF=BF,
∵AB=AC,點D是BC的中點,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中, ,
,
∴△AEF≌△BCF(ASA).
【點評】本題考查了全等三角形的判定與性質,等腰三角形三線合一的性質,等腰直角三角形的判定與性質,同角的余角相等的性質,是基礎題,熟記三角形全等的判定方法與各性質是解題的關鍵.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
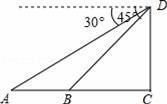
如圖,為了測量河的寬度AB,測量人員在高21m的建筑物CD的頂端D處測得河岸B處的俯角為45°,測得河對岸A處的俯角為30°(A、B、C在同一條直線上),則河的寬度AB約是多少m?(精確到0.1m).(參考數據: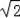
 ≈1.41,
≈1.41,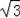
 ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
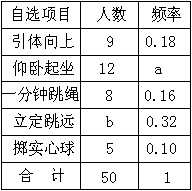
某校九年級(1)班50名學生需要參加“五選一”自選項目測試,班上學生
所報自選項目的情況統計表如下:
(1)求a、b的值.
(2)若將各自選項目的人數所占比例繪制成扇形統計圖,求一分鐘跳繩對應扇形的圓心角的度數.
(3)在選報擲實心球的學生中,有3名男生,2名女生為了了解學生的訓練效果,從這5名學生中隨機抽取兩名學生進行擲實心球測試,求所抽取的兩名學生中至多有一名女生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com