
【題目】已知在平面直角坐標系xOy中,直線y=2x+2和直線y=![]() x+2分別交x軸于點A和點B.則下列直線中,與x軸的交點不在線段AB上的直線是( )
x+2分別交x軸于點A和點B.則下列直線中,與x軸的交點不在線段AB上的直線是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,菱形ABCD如圖所示,![]() ,點D在線段AB的垂直平分線上,若菱形ABCD繞點O逆時針旋轉,旋轉速度為每秒
,點D在線段AB的垂直平分線上,若菱形ABCD繞點O逆時針旋轉,旋轉速度為每秒![]() ,則第70秒時點D的對應坐標為( )
,則第70秒時點D的對應坐標為( )
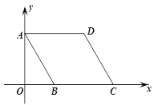
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0)交于A、B兩點,A點的橫坐標為3,則下列結論:①k=6;②A點與B點關于原點O中心對稱;③關于x的不等式
(k>0)交于A、B兩點,A點的橫坐標為3,則下列結論:①k=6;②A點與B點關于原點O中心對稱;③關于x的不等式![]() <0的解集為x<﹣3或0<x<3;④若雙曲線y=
<0的解集為x<﹣3或0<x<3;④若雙曲線y=![]() (k>0)上有一點C的縱坐標為6,則△AOC的面積為8,其中正確結論的個數( )
(k>0)上有一點C的縱坐標為6,則△AOC的面積為8,其中正確結論的個數( )
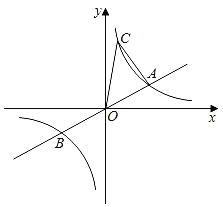
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新龜兔賽跑的故事:龜兔從同一地點同時出發后,兔子很快把烏龜遠遠甩在后頭.驕傲自滿的兔子覺得自己遙遙領先,就躺在路邊呼呼大睡起來.當它一覺醒來,發現烏龜已經超過它,于是奮力直追,最后同時到達終點.用S1、S2分別表示烏龜和兔子賽跑的路程,t為賽跑時間,則下列圖象中與故事情節相吻合的是( )
A.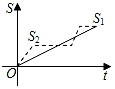 B.
B.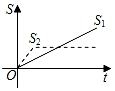
C.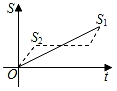 D.
D.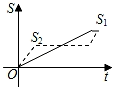
查看答案和解析>>
科目:初中數學 來源: 題型:
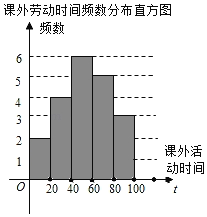
【題目】遵義市各校都在深入開展勞動教育,某校為了解七年級學生一學期參加課外勞動時間(單位:h)的情況,從該校七年級隨機抽查了部分學生進行問卷調查,并將調查結果繪制成如下不完整的頻數分布表和頻數分布直方圖.
課外勞動時間頻數分布表
勞動時間分組 | 頻數 | 頻率 |
0≤t<20 | 2 | 0.1 |
20≤t<40 | 4 | m |
40≤t<60 | 6 | 0.3 |
60≤t<80 | a | 0.25 |
80≤t<100 | 3 | 0.15 |
解答下列問題:
(1)頻數分布表中a= ,m= ;將頻數分布直方圖補充完整;
(2)若七年級共有學生400人,試估計該校七年級學生一學期課外勞動時間不少于60h的人數;
(3)已知課外勞動時間在60h≤t<80h的男生人數為2人,其余為女生,現從該組中任選2人代表學校參加“全市中學生勞動體驗”演講比賽,請用樹狀圖或列表法求所選學生為1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生對網上在線學習效果的滿意度,某校設置了:非常滿意、滿意、基本滿意、不滿意四個選項,隨機抽查了部分學生,要求每名學生都只選其中的一項,并將抽查結果繪制成如圖統計圖(不完整).
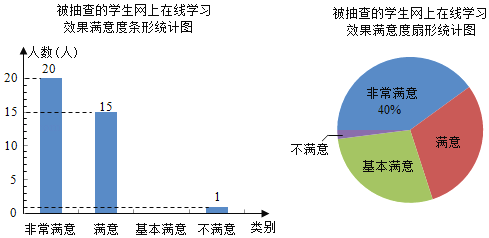
請根據圖中信息解答下列問題:
(1)求被抽查的學生人數,并補全條形統計圖;(溫馨提示:請畫在答題卷相對應的圖上)
(2)求扇形統計圖中表示“滿意”的扇形的圓心角度數;
(3)若該校共有1000名學生參與網上在線學習,根據抽查結果,試估計該校對學習效果的滿意度是“非常滿意”或“滿意”的學生共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經過實驗獲得兩個變量x(x>0),y(y>0)的一組對應值如下表.
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
(1)請畫出相應函數的圖象,并求出函數表達式.
(2)點A(x1,y1),B(x2,y2)在此函數圖象上.若x1<x2,則y1,y2有怎樣的大小關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒肺炎的防護知識,并鼓勵社區居民在線參與作答《2020年新型冠狀病毒防治全國統一考試(全國卷)》試卷(滿分100分),社區管理員隨機從有400人的某小區抽取40名人員的答卷成績,并對他們的成績(單位:分)統計如下:
85 80 95 100 90 95 85 65 75 85
90 90 70 90 100 80 80 90 95 75
80 60 80 95 85 100 90 85 85 80
95 75 80 90 70 80 95 75 100 90
根據數據繪制了如下的表格和統計圖:
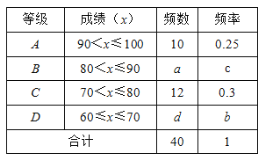
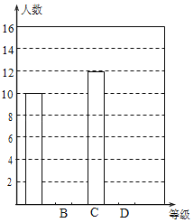
根據上面提供的信息,回答下列問題:
(1)統計表中的a= ,b= ;c= ,d=
(2)請補全條形統計圖;
(3)根據抽樣調查結果,請估計該小區答題成績為“C級”的有多少人?
(4)該社區有2名男管理員和2名女管理員,現從中隨機挑選2名管理員參加“社區防控”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖①,在矩形![]() 中,
中,![]() ,垂足是
,垂足是![]() .點
.點![]() 是點
是點![]() 關于
關于![]() 的對稱點,連接
的對稱點,連接![]()
![]() .
.
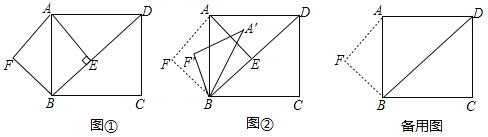
(1)求![]() 和
和![]() 的長;
的長;
(2)若將![]() 沿著射線
沿著射線![]() 方向平移,設平移的距離為
方向平移,設平移的距離為![]() (平移距離指點
(平移距離指點![]() 沿
沿![]() 方向所經過的線段長度).當點
方向所經過的線段長度).當點![]() 分別平移到線段
分別平移到線段![]() 上時,直接寫出相應的
上時,直接寫出相應的![]() 的值.
的值.
(3)如圖②,將![]() 繞點
繞點![]() 順時針旋轉一個角
順時針旋轉一個角![]() ,記旋轉中
,記旋轉中![]() 為
為![]() ,在旋轉過程中,設
,在旋轉過程中,設![]() 所在的直線與直線
所在的直線與直線![]() 交于點
交于點![]() ,與直線
,與直線![]() 交于點
交于點![]() .是否存在這樣的
.是否存在這樣的![]() 兩點,使
兩點,使![]() 為等腰三角形?若存在,求出此時
為等腰三角形?若存在,求出此時![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com