【題目】平面上5個圓最多能把平面分成多少個部分？一般地，n個圓最多能把平面分成多少個部分？
【答案】5個圓最多將平面分成22個部分，n個圓最多分平面為n2﹣n+2．
【解析】
根據題意，探索出圓的個數與分成的平面個數的關系，從而得出結論.
1個圓最多能把平面分成2個部分，
2個圓最多能把平面分成4個部分；
3個圓最多能把平面分成8個部分；
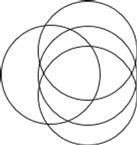
現在加入第4個圓，為了使分成的部分最多，第4個圓必須與前面3個圓都有兩個交點，
如圖所示，因此得6個交點將第4個圓的圓周分成6段圓弧，而每一段圓弧將原來的部分一分為二，即增加了一個部分，于是4個圓最多將平面分成8+6＝14個部分，
同理，5個圓最多將平面分成14+8＝22個部分，
一般地，n個圓最多分平面為：
2+1×2+2×2+…+（n﹣1）×2，
＝2+2[1+2+…+（n﹣1）]，
＝n2﹣n+2．
科目：初中數學 來源： 題型：
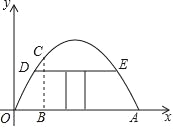
【題目】有一個拋物線型蔬菜大棚，將其截面放在如圖所示的平面直角坐標系中，拋物線可以用函數y＝ax2+bx來表示，已知OA＝8米，距離O點2米處的棚高BC為
米．
（1）求該拋物線的解析式；
（2）若借助橫梁DE（DE∥OA）建一個門，要求門的高度為1.5米，求橫梁DE的長度是多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
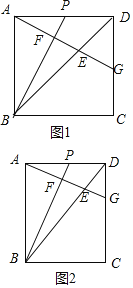
【題目】在矩形ABCD中，P是AD的中點，連BP，過A作BP的垂線，垂足為F，交BD于E，交CD于G．
（1）若矩形ABCD是正方形，如圖1，
①求證：AG＝BP．
②
的值為 ．
（2）類比：如圖2，在矩形ABCD中，若2AB＝3AD，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（問題背景）先閱讀理解下面的例題，再按要求解答下列問題：
例題：解一元二次不等式x2﹣4＞0
（問題解決）∵x2﹣4＝（x+2）（x﹣2）
∴x2﹣4＞0可化為（x+2）（x﹣2）＞0
由有理數的乘法法則“兩數相乘，同號得正”，得
解不等式組①，得x＞2，
解不等式組②，得x＜﹣2，
∴（x+2）（x﹣2）＞0的解集為x＞2或x＜﹣2，
即一元二次不等式 x2﹣4＞0 的解集為x＞2或x＜﹣2．
（問題應用）（1）一元二次不等式 x2﹣16＞0 的解集為 ；
（2）分式不等式
＞0 的解集為 ；
（3）（拓展應用）解一元二次不等式 2x2﹣3x＜0．
查看答案和解析>>
科目：初中數學 來源： 題型：
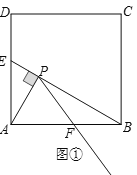
【題目】如圖，正方形ABCD的邊長是6，點E、F分別是邊AD、AB的點,AP⊥BE于點P.
(1)如圖①，當AE=2
且AF=BF時，若點T是射線PF上的一個動點(點T不與點P重合)，當△ABT是直角三角形時，求AT的長.
(2)如圖②，當AE=AF時，連結CP，判斷CP與PF的位置關系，并加以證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋一枚均勻硬幣正面朝上的概率為
，下列說法錯誤的是
A. 連續拋一枚均勻硬幣2次必有1次正面朝上
B. 連續拋一枚均勻硬幣10次都可能正面朝上
C. 大量反復拋一枚均勻硬幣，平均每100次出現正面朝上50次
D. 通過拋一枚均勻硬幣確定誰先發球的比賽規則是公平的
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】矩形ABCD與CEFG，如圖放置，點B，C，E共線，點C，D，G共線，連接AF，取AF的中點H，連接GH．若BC=EF=2，CD=CE=1，則GH=（ ）
A. 1 B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個不透明的盒子中，裝有2個白球和1個紅球，這些球除顏色外其余都相同.
(1)你同意下列說法嗎？請說明理由.
①攪勻后從中任意摸出一個球，不是白球就是紅球，因此摸出白球和摸出紅球這兩個事件是等可能的.
②如果將摸出的第一個球放回攪勻后再摸出第二個球，兩次摸球就可能出現3種結果，即“都是紅球”、“都是白球”、“一紅一白”.這三個事件發生的概率相等.
(2)攪勻后從中任意摸出一個球，要使摸出紅球的概率為
，應如何添加紅球？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線y＝3x2+bx+c與直線y＝﹣1只有一個公共點M，與平行于x軸的直線l交此拋物線A，B兩點若AB=4，則點M到直線l的距離為（ ）
A.11B.12C.
D.13
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com