
【題目】如圖,等邊△OAB和等邊△AFE的一邊都在x軸上,雙曲線y=![]() (k>0)經過邊OB的中點C和AE的中點D.已知等邊△OAB的邊長為4.
(k>0)經過邊OB的中點C和AE的中點D.已知等邊△OAB的邊長為4.
(1)求該雙曲線所表示的函數解析式;
(2)求等邊△AEF的邊長.

【答案】解:(1) 過點C作CG⊥OA于點G,

∵點C是等邊△OAB的邊OB的中點,
∴OC=2,∠ AOB=60°。∴OG=1,CG=![]() ,
,
∴點C的坐標是(1, ![]() )。由
)。由![]() ,得:k=
,得:k=![]() 。
。
∴該雙曲線所表示的函數解析式為![]() 。
。
(2) 過點D作DH⊥AF于點H,設AH=a,則DH=![]() a。
a。
∴點D的坐標為(4+a, ![]() a)。
a)。
∵點D是雙曲線![]() 上的點,
上的點,
∴由xy=![]() ,得
,得![]() a (4+a)=
a (4+a)=![]() ,即:a2+4a-1=0。
,即:a2+4a-1=0。
解得:a1=![]() -2,a2=-
-2,a2=-![]() -2(舍去)。∴AD=2AH=2
-2(舍去)。∴AD=2AH=2![]() -4。
-4。
∴等邊△AEF的邊長是2AD=4![]() -8。.
-8。.
【解析】(1)過點C作CG⊥OA于點G,根據等邊三角形的性質求出OG、CG的長度,從而得到點C的坐標,再利用待定系數法求反比例函數解析式列式計算即可得解。
(2)過點D作DH⊥AF于點H,設AH=a,根據等邊三角形的性質表示出DH的長度,然后表示出點D的坐標,再把點D的坐標代入反比例函數解析式,解方程得到a的值,從而得解。


科目:初中數學 來源: 題型:
【題目】計算(x﹣1)(2x+1)﹣(x2+x﹣2)的結果,與下列哪一個式子相同( )
A.x2﹣2x﹣3
B.x2﹣2x+1
C.x2+x﹣3
D.x2﹣3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,F是AD的中點,延長BC到點E,使CE=![]() BC,連接DE,CF.
BC,連接DE,CF.
(1)求證:四邊形CEDF是平行四邊形;
(2)若AB=4,AD=6,∠B=60°,求DE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖甲,在△ABC中,∠ACB為銳角,點D為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF.解答下列問題: 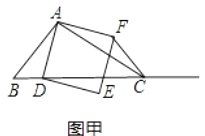
(1)如果AB=AC,∠BAC=90°, ①當點D在線段BC上時(與點B不重合),如圖乙,線段CF、BD之間的位置關系為 , 數量關系為 .
②當點D在線段BC的延長線上時,如圖丙,①中的結論是否仍然成立,為什么?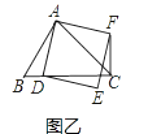
(2)如果AB≠AC,∠BAC≠90°點D在線段BC上運動.試探究:當△ABC滿足一個什么條件時,CF⊥BC(點C、F重合除外)?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖某農場要建一個長方形的養雞場,雞場的一邊靠墻(墻長18m),另三邊用木欄圍成,木欄長35m.雞場的面積能達到150m2嗎?如果能,請你給出設計方案;如果不能,請說明理由. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉辦校級籃球賽,進入決賽的隊伍有A、B、C、D,要從中選出兩隊打一場比賽.
(1)若已確定A打第一場,再從其余三隊中隨機選取一隊,求恰好選中D隊的概率.
(2)請用畫樹狀圖或列表法,求恰好選中B、C兩隊進行比賽的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com