
【題目】若一個數能表示成某個整數的平方的形式,則稱這個數為完全平方數,完全平方數是非負數.例如:0=02,1=12,4=22,9=32,16=42,25=52,36=62,121=112….
(1)若28+210+2n是完全平方數,求n的值.
(2)若一個正整數,它加上61是一個完全平方數,當減去11是另一個完全平方數,寫出所有符合的正整數.
【答案】(1)n=4或n=10;(2)所有符合的正整數是20、60或300.
【解析】
(1)直接利用a+2ab+b=(a+b) ,分別使每一項與公式對應即分3種情況求出n的值即可;
(2)根據題意,設正整數為x,則x+61=a,x-11=b,進而得出關于a,b的等式,再分別討論求出答案即可.
(1)解:∵a2+b2+2ab=(a+b)2,
∴若28=a2,210=b2,
則a=24,b=25,2n=2ab=210,解得:n=10
若28=a2,210=2ab,
所以b=25,
則2n=b2=210,
解得:n=10,
若210=a2,28=2ab,
所以b=22,
則2n=b2=24,
解得:n=4,
所以n=4或n=10;
(2)解:設正整數為x,則x+61=a2,x﹣11=b2(a>b,且a,b是正整數),
則a2﹣b2=x+61﹣x+11=72,
故(a+b)(a﹣b)=72,
由于a+b與a﹣b同奇偶,
故![]() 或
或![]() 或者
或者![]() ,
,
當![]() 時,
時,
解得:![]() ,
,
∴x=b2+11=60;
當![]() 時,
時,
解得:![]() ,
,
∴x=b2+11=300;
當![]() 時,
時,
解得:![]() ,
,
∴x=b2+11=20.
所以所有符合的正整數是20、60或300.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分線相交于點O,OM∥AB,ON∥AC分別與BC交于點M、N,則△OMN的周長為____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設(a,b)是一次函數y=(k-2)x+m與反比例函數![]() 的圖象的交點,且a、b是關于x的一元二次方程
的圖象的交點,且a、b是關于x的一元二次方程![]() 的兩個不相等的實數根,其中k為非負整數,m、n為常數.
的兩個不相等的實數根,其中k為非負整數,m、n為常數.
(1)求k的值;
(2)求一次函數與反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c過點A(﹣3,0),B(﹣2,3),C(0,3),頂點為D.
(1)求拋物線的解析式;
(2)設點M(1,m),當MB+MD的值最小時,求m的值;
(3)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,其中A點坐標為(-1,0),B點坐標為(5,0)點C(0,5),M為它的頂點.
(1)求拋物線的解析式;
(2)求△MAB的面積。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七(1)班同學為了解2018年某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行如下整理,請解答以下問題:

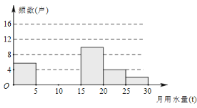
(1)求![]() ,
,![]() 的值.并把頻數直方圖補充完整;
的值.并把頻數直方圖補充完整;
(2)求該小區用水量不超過![]() 的家庭占被調在家庭總數的百分比;
的家庭占被調在家庭總數的百分比;
(3)若該小區有1000戶家庭,根據調查數據估計,該小區月均用水是超過![]() 的家庭大約有多少戶?
的家庭大約有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區將原來400平方米的正方形場地改建成300平方米的長方形場地,且長和寬之比為3∶2.如果把原來正方形場地的鐵柵欄圍墻利用起來圍成新場地的長方形圍墻,那么這些鐵柵欄是否夠用?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足為A,B,連接AB,下列結論中不一定成立的是( )

A.PA=PBB.PO平分∠APBC.OA=OBD.AB平分OP
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,∠MON=30°,點A1、A2、A3在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=a,則△A7B7A8的邊長為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com