
【題目】如圖所示,一段街道的兩邊沿所在直線分別為AB,PQ,并且AB∥PQ,建筑物的一端DE所在的直線MN⊥AB于點M,交PQ于點N,小亮從勝利街的A處,沿著AB方向前進,小明一直站在點P的位置等待小亮.
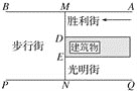
(1)請你畫出小亮恰好能看見小明的視線,以及此時小亮所在的位置(用點C標出).
(2)已知:MN=30 m,MD=12 m,PN=36 m.求(1)中的點C到勝利街口的距離.
 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數(shù)學 來源: 題型:
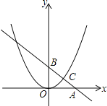
【題目】已知,如圖,在平面直角坐標系中,△ABC是直角三角形,∠ACB=90°,點A、C的坐標分別為A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求點B的坐標;
(2)在x軸上找一點D,連接BD使得△ABD與△ABC相似(不包括全等),并求點D的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線y=kx+b(k、b為常數(shù))分別與x軸、y軸交于點A(﹣4,0)、B(0,3),拋物線y=﹣x2+2x+1與y軸交于點C,點E在拋物線y=﹣x2+2x+1的對稱軸上移動,點F在直線AB上移動,CE+EF的最小值是( )
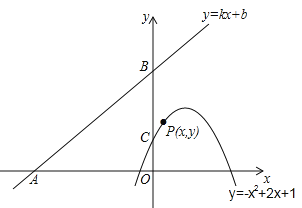
A. 1.4 B. 2.5 C. 2.8 D. 3
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6,BC=8,動點P在邊AD上以每秒2個單位的速度從A出發(fā),沿AD向D運動,同時動點Q在邊BD上以每秒5個單位的速度從D出發(fā),沿DB向B運動,當其中有一個點到達終點時,另一個點也隨之停止運動.設運動時間為t秒.
(1)填空:當某一時刻t,使得t=1時,P、Q兩點間的距離PQ= ;
(2)是否存在以P、D、Q中一點為圓心的圓恰好過另外兩個點?若存在求出此時t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,某足球運動員站在點O處練習射門,將足球從離地面0.5m的A處正對球門踢出(點A在y軸上),足球的飛行高度y(單位:m)與飛行時間t(單位:s)之間滿足函數(shù)關系y=at2+5t+c,已知足球飛行0.8s時,離地面的高度為3.5m.
(1)足球飛行的時間是多少時,足球離地面最高?最大高度是多少?
(2)若足球飛行的水平距離x(單位:m)與飛行時間t(單位:s)之間具有函數(shù)關系x=10t,已知球門的高度為2.44m,如果該運動員正對球門射門時,離球門的水平距離為28m,他能否將球直接射入球門?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,直線![]() 交坐標軸于
交坐標軸于![]() 、
、![]() 兩點,交拋物線
兩點,交拋物線![]() 于點
于點![]() ,且
,且![]() 是線段
是線段![]() 的中點,拋物線上另有位于第一象限內(nèi)的一點
的中點,拋物線上另有位于第一象限內(nèi)的一點![]() ,過
,過![]() 的直線
的直線![]() 交坐標軸于
交坐標軸于![]() 、
、![]() 兩點,且
兩點,且![]() 恰好是線段
恰好是線段![]() 的中點,若
的中點,若![]() ,則
,則![]() 點的坐標是________.
點的坐標是________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】二次函數(shù)的圖象通過![]() 和
和![]() 兩點,但不通過直線
兩點,但不通過直線![]() 上方的點,則其頂點縱坐標的最大值與最小值的乘積為( )
上方的點,則其頂點縱坐標的最大值與最小值的乘積為( )
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖⊙O的內(nèi)接△ABC中,外角∠ACF的角平分線與⊙O相交于D點,DP⊥AC,垂足為P,DH⊥BF,垂足為H.問:
(1)∠PDC與∠HDC是否相等,為什么?
(2)圖中有哪幾組相等的線段?
(3)當△ABC滿足什么條件時,△CPD∽△CBA,為什么?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
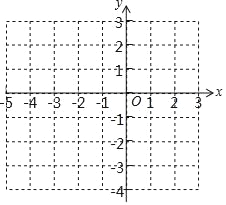
【題目】一個二次函數(shù)圖象上部分點的橫坐標x,縱坐標y的對應值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求這個二次函數(shù)的表達式;
(2)求m的值;
(3)在給定的直角坐標系中,畫出這個函數(shù)的圖象;
(4)根據(jù)圖象,寫出當y<0時,x的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com