
【題目】如圖,直線y=kx+b(k、b為常數)分別與x軸、y軸交于點A(﹣4,0)、B(0,3),拋物線y=﹣x2+2x+1與y軸交于點C,點E在拋物線y=﹣x2+2x+1的對稱軸上移動,點F在直線AB上移動,CE+EF的最小值是( )
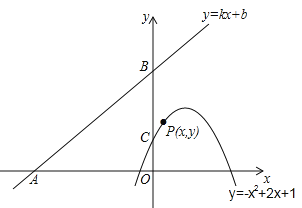
A. 1.4 B. 2.5 C. 2.8 D. 3
【答案】C
【解析】分析:由A、B兩點的坐標,利用待定系數法可求得直線解析式;過P作PH⊥AB于點H,過H作HQ⊥x軸,過P作PQ⊥y軸,兩垂線交于點Q,則可證明△PHQ∽△BAO,設H(m, ![]() m+3),利用相似三角形的性質可得到d與x的函數關系式,設C點關于拋物線對稱軸的對稱點為C′,由對稱的性質可得CE=C′E,則可知當F、E、C′三點一線且C′F與AB垂直時CE+EF最小,由C點坐標可確定出C′點的坐標,利用所求函數關系式可求得d的值,即可求得CE+EF的最小值.
m+3),利用相似三角形的性質可得到d與x的函數關系式,設C點關于拋物線對稱軸的對稱點為C′,由對稱的性質可得CE=C′E,則可知當F、E、C′三點一線且C′F與AB垂直時CE+EF最小,由C點坐標可確定出C′點的坐標,利用所求函數關系式可求得d的值,即可求得CE+EF的最小值.
詳解: (1)由題意可得
![]() ,解得
,解得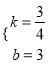 ,
,
∴直線解析式為y=![]() x+3;
x+3;
過P作PH⊥AB于點H,過H作HQ⊥x軸,過P作PQ⊥y軸,兩垂線交于點Q,
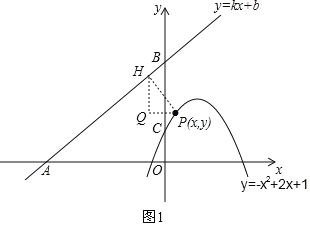
則∠AHQ=∠ABO,且∠AHP=90°,
∴∠PHQ+∠AHQ=∠BAO+∠ABO=90°,
∴∠PHQ=∠BAO,且∠AOB=∠PQH=90°,
∴△PQH∽△BOA,
∴![]() ,
,
設H(m, ![]() m+3),則PQ=xm,HQ=
m+3),則PQ=xm,HQ=![]() m+3(x+2x+1),
m+3(x+2x+1),
∵A(4,0),B(0,3),
∴OA=4,OB=3,AB=5,且PH=d,
∴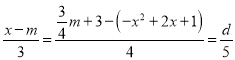
整理消去m可得d=![]() ,
,
∴d與x的函數關系式為d=![]() ,
,
設C點關于拋物線對稱軸的對稱點為C′,由對稱的性質可得CE=C′E,
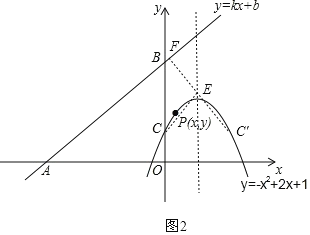
∴CE+EF=C′E+EF,
∴當F. E.C′三點一線且C′F與AB垂直時CE+EF最小,
∵C(0,1),
∴C′(2,1),
由(2)可知當x=2時,d=![]() =2.8,
=2.8,
即CE+EF的最小值為2.8.
點睛:
本題為二次函數的綜合應用,涉及待定系數法、相似三角形的判定和性質、二次函數的性質、軸對稱的性質等知識.注意待定系數法的應用,構造相似三角形是解題的重要步驟,確定出E點的位置是解題的關鍵.本題考查知點較多,綜合性較強,難度適中.


科目:初中數學 來源: 題型:
【題目】某校八年級學生小麗、小強和小紅到某超市參加了社會實踐活動,在活動中他們參與了某種水果的銷售工作.已知該水果的進價為8元/千克,下面是他們在活動結束后的對話.
小麗:如果以10元/千克的價格銷售,那么每天可售出300千克.
小強:如果每千克的利潤為3元,那么每天可售出250千克.
小紅:如果以13元/千克的價格銷售,那么每天可獲取利潤750元.
【利潤=(銷售價-進價)![]() 銷售量】
銷售量】
(1)請根據他們的對話填寫下表:
銷售單價x(元/kg) | 10 | 11 | 13 |
銷售量y(kg) |
(2)請你根據表格中的信息判斷每天的銷售量y(千克)與銷售單價x(元)之間存在怎樣的函數關系.并求y(千克)與x(元)(x>0)的函數關系式;
(3)設該超市銷售這種水果每天獲取的利潤為W元,求W與x的函數關系式.當銷售單價為何值時,每天可獲得的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上![]() 點表示數
點表示數![]() ,
,![]() 點表示數6,
點表示數6,
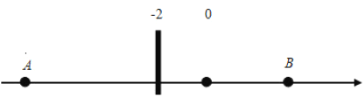
(1)A、B兩點之間的距離等于_________;
(2)在數軸上有一個動點![]() ,它表示的數是
,它表示的數是![]() ,則
,則![]() 的最小值是_________;
的最小值是_________;
(3)若點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,請在數軸上找一點
,請在數軸上找一點![]() ,使
,使![]() ,則
,則![]() 點表示的數是_________;
點表示的數是_________;
(4)若在原點![]() 的左邊2個單位處放一擋板,一小球甲從點
的左邊2個單位處放一擋板,一小球甲從點![]() 處以5個單位/秒的速度向右運動;同時另一小球乙從點
處以5個單位/秒的速度向右運動;同時另一小球乙從點![]() 處以2個單位/秒的速度向左運動,在碰到擋板后(忽略球的大小,可看作一點)兩球分別以原來的速度向相反的方向運動,設運動時間為
處以2個單位/秒的速度向左運動,在碰到擋板后(忽略球的大小,可看作一點)兩球分別以原來的速度向相反的方向運動,設運動時間為![]() 秒,請用
秒,請用![]() 來表示甲、乙兩小球之間的距離
來表示甲、乙兩小球之間的距離![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個直角三角形紙片ABO放置在平面直角坐標系中,點A(![]() ,0),點B(0,1),點O(0,0).P是邊AB上的一點(點P不與點A,B重合),沿著OP折疊該紙片,得點A的對應點A',當∠BPA'=30°時,點P的坐標為______.
,0),點B(0,1),點O(0,0).P是邊AB上的一點(點P不與點A,B重合),沿著OP折疊該紙片,得點A的對應點A',當∠BPA'=30°時,點P的坐標為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度數;
(2)若∠DOE=n°,求∠AOB的度數;
(3)若∠DOE+∠AOB=180°,求∠AOB與∠DOE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
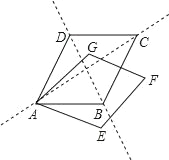
【題目】如圖,菱形ABCD和菱形AEFG開始完全重合,現將菱形AEFG繞點A順時針旋轉,設旋轉角∠BAE=α(0°<α<360°),則當α=_____時,菱形的頂點F會落在菱形ABCD的對角線所在的直線上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【探索發現】
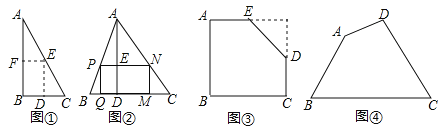
如圖①,是一張直角三角形紙片,∠B=60°,小明想從中剪出一個以∠B為內角且面積最大的矩形,經過多次操作發現,當沿著中位線DE、EF剪下時,所得的矩形的面積最大,隨后,他通過證明驗證了其正確性,并得出:矩形的最大面積與原三角形面積的比值為 .
【拓展應用】
如圖②,在△ABC中,BC=a,BC邊上的高AD=h,矩形PQMN的頂點P、N分別在邊AB、AC上,頂點Q、M在邊BC上,則矩形PQMN面積的最大值為 .(用含a,h的代數式表示)
【靈活應用】
如圖③,有一塊“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明從中剪出了一個面積最大的矩形(∠B為所剪出矩形的內角),求該矩形的面積.
【實際應用】
如圖④,現有一塊四邊形的木板余料ABCD,經測量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
,木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com