
【題目】如圖1,在平面直角坐標系中,直線y=-![]() x-
x-![]() 與x軸交于點A,與y軸交于點B,點C在x軸正半軸上,且OC=3AO,過點A作BC的平行線l.
與x軸交于點A,與y軸交于點B,點C在x軸正半軸上,且OC=3AO,過點A作BC的平行線l.
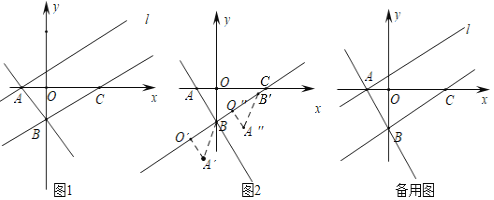
(1)求直線BC的解析式;
(2)作點A關于BC的對稱點D,一動點P從C點出發按某一路徑運動到直線l上的點M,再沿垂直BC的方向運動到直線BC上的點N,再沿某一路徑運動到D點,求點P運動的最短路徑的長以及此時點N的坐標;
(3)如圖2,將△AOB繞點B旋轉,使得A′O′⊥BC,得到△A′O′B,將△A′O′B沿直線BC平移得到△A″O″B′,連接A″、B″、C,是否存在點A″,使得△A″B′C為等腰三角形?若存在,請直接寫出點A″的坐標;若不存在,請說明理由.
【答案】(1) y=![]() x-
x-![]() ;(2) 2
;(2) 2![]() , N(
, N(![]() ,-
,-![]() );(3)見解析.
);(3)見解析.
【解析】
(1)利用待定系數法即可解決問題;
(2)如圖2中,作點C關于直線AF的對稱點C′,連接CC′交AF于點F,連接DF交BC于N,作NE⊥AF于E,連接EC,則此時CE+EN+DN的值最小,最小值=線段DF的長;
(3)分四種情形分別畫出圖形求解即可.
(1)∵直線y=-![]() x-
x-![]() 與x軸交于點A,與y軸交于點B,
與x軸交于點A,與y軸交于點B,
∴A(-1,0),B(0,-![]() ),
),
∵OC=3OA,
∴OC=3,
∴C(3,0),
設直線BC的解析式為y=kx+b,則有![]() ,
,
解得 ,
,
∴直線BC的解析式為y=![]() x-
x-![]() ;
;
(2)如圖2中,作點C關于直線AF的對稱點C′,連接CC′交AF于點F,連接DF交BC于N,作NE⊥AF于E,連接EC,則此時CE+EN+DN的值最小,最小值=線段DF的長.

由題意D(1,-2![]() ),
),
∵直線CF的解析式為y=![]() x+
x+![]() ,直線CF的解析式為y=-
,直線CF的解析式為y=-![]() x+3
x+3![]() ,
,
由 ,解得
,解得![]() ,
,
∴F(2,![]() ),
),
∴DF=![]() =2
=2![]() ,
,
∴點P的路徑的最小值為2![]() ,
,
∵直線DF的解析式為y=3![]() x-5
x-5![]() ,
,
由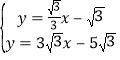 ,解得
,解得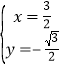 ,
,
∴N(![]() ,-
,-![]() );
);
(3)由題意,BO′=BO=![]() ,AB=BA′=2,OA=O′A′=1,點O′向下平移
,AB=BA′=2,OA=O′A′=1,點O′向下平移![]() 個單位,向右平移
個單位,向右平移![]() 單位得到A′,
單位得到A′,
①如圖3中,當CB′=B′A″=2時,此時O″(![]() ,-
,-![]() ),可得A″(2-
),可得A″(2-![]() ,-1-
,-1-![]() ).
).
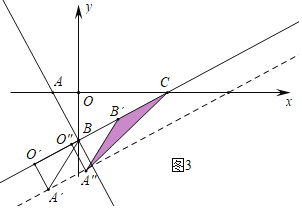
②如圖4中,當CB′=CA″時,設CB′=CA″=x,則有x2=12+(![]() -x)2,
-x)2,
可得x=![]() ,此時O″(
,此時O″(![]() ,-
,-![]() ),可得A″(3,-
),可得A″(3,-![]() ).
).
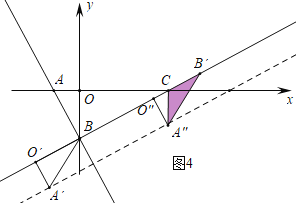
③當B′C=B′A″=2時,O″(![]() ,
,![]() ),可得A″(2+
),可得A″(2+![]() ,1-
,1-![]() )
)
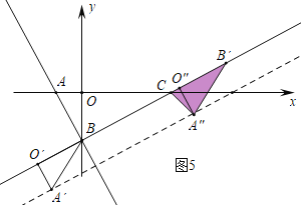
④當CA″=B′A″=2時,O″(![]() ,
,![]() ),可得A″(5,0).
),可得A″(5,0).
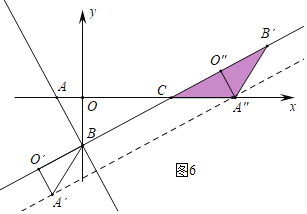
綜上所述,滿足條件的點A″的坐標為(2-![]() ,-1-
,-1-![]() )或(3,-
)或(3,-![]() )或(2+
)或(2+![]() ,1-
,1-![]() )或(5,0).
)或(5,0).


科目:初中數學 來源: 題型:
【題目】電力公司為鼓勵市民節約用電,采取按月用電量分段收費辦法.若某戶居民每月應交電費y(元)與用電量x(度)的函數圖象是一條折線(如圖所示),根據圖象解下列問題:
(1) 分別寫出當0≤x≤100和x>100時,y與x的函數關系式
(2) 利用函數關系式,說明電力公司采取的收費標準
(3) 若該用戶某月用電62度,則應繳費多少元?若該用戶某月繳費105元時,則該用戶該月用了多少度電?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和父親在一直線公路AB上進行(A→B→A)往返跑訓練,兩人同時從A點出發,父親以較快的速度勻速跑到點B休息2分鐘后立即原速跑回A點,小明先勻速慢跑了3分鐘后,把速度提高到原來的![]() 倍,又經過6分鐘后超越了父親一段距離,小明又將速度降低到出發時的速度,并以這一速度勻速跑到B點看到休息的父親,然后立即以出發時的速度跑回A點,若兩人之間的距離記為y(米),小明的跑步時間記為x(分),y和x的部分函數關系如圖所示,則當父親回到A點時小明距A點______米.
倍,又經過6分鐘后超越了父親一段距離,小明又將速度降低到出發時的速度,并以這一速度勻速跑到B點看到休息的父親,然后立即以出發時的速度跑回A點,若兩人之間的距離記為y(米),小明的跑步時間記為x(分),y和x的部分函數關系如圖所示,則當父親回到A點時小明距A點______米.
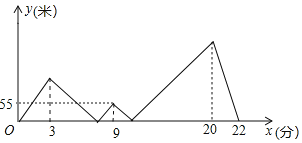
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若關于x的一元二次方程(x-2)(x-3)=m有實數根x1 , x2 , 且x1![]() x2有下列結論:①x1=2,x2=3;②m>
x2有下列結論:①x1=2,x2=3;②m> ![]() ;③二次函數y=(x-x1)(x-x2)+m的圖象與x軸交點的坐標為(2,0)和(3,0).其中正確的結論是(填正確結論的序號)
;③二次函數y=(x-x1)(x-x2)+m的圖象與x軸交點的坐標為(2,0)和(3,0).其中正確的結論是(填正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
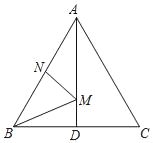
【題目】如圖,在等邊△ABC中,AB=2,N為AB上一點,且AN=1,AD=![]() ,∠BAC的平分線交BC于點D,M是AD上的動點,連接BM、MN,則BM+MN的最小值是( )
,∠BAC的平分線交BC于點D,M是AD上的動點,連接BM、MN,則BM+MN的最小值是( )
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,點![]() 在
在![]() 軸正半軸,點
軸正半軸,點![]() 在
在![]() 軸負半軸,連接
軸負半軸,連接![]() ,
,![]() ,
,![]()
(1)求點![]() 坐標
坐標
(2)如圖2,點![]() 是線段
是線段![]() 上一點,連接
上一點,連接![]() ,以
,以![]() 為直角邊做等腰直角
為直角邊做等腰直角![]() ,
,![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,求點
,求點![]() 的坐標(用含
的坐標(用含![]() 的代數式表示)
的代數式表示)
(3)在(2)的條件下,如圖3,在![]() 延長線上有一點
延長線上有一點![]() ,過點
,過點![]() 作
作![]() 的平行線,交
的平行線,交![]() 軸于點
軸于點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,求點
,求點![]() 的坐標.
的坐標.



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com