
【題目】已知![]() ,
,![]() 、
、![]() 、
、![]() 的對邊分別是
的對邊分別是![]() 、
、![]() 、
、![]() ,一條直線
,一條直線![]() 與邊
與邊![]() 相交于點
相交于點![]() ,與邊
,與邊![]() 相交于點
相交于點![]() .
.
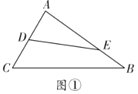
(1)如圖①,若![]() 將
將![]() 分成周長相等的兩部分,求
分成周長相等的兩部分,求![]() 的值;(用
的值;(用![]() 、
、![]() 、
、![]() 表示)
表示)
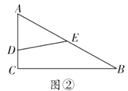
(2)如圖②,若![]() ,
,![]() ,
,![]() ,
,![]() 將
將![]() 分成周長、面積相等的兩部分,求
分成周長、面積相等的兩部分,求![]() 的值;
的值;
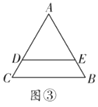
(3)如圖③,若![]() 將
將![]() 分成周長、面積相等的兩部分,且
分成周長、面積相等的兩部分,且![]() ,則
,則![]() 、
、![]() 、
、![]() 滿足什么關系?
滿足什么關系?
科目:初中數學 來源: 題型:
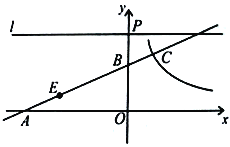
【題目】已知:如圖,直線![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,與
,與![]() 軸正半軸交于點
軸正半軸交于點![]() ,線段
,線段![]() 的長是方程
的長是方程![]() 的一個根,請解答下列問題:
的一個根,請解答下列問題:
(1)求點![]() 的坐標;
的坐標;
(2)雙曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,點![]() 在線段
在線段![]() 上,
上,![]() ,直線
,直線![]() 軸,垂足為
軸,垂足為![]() ,點
,點![]() 在直線
在直線![]() 上,在直線
上,在直線![]() 上的坐標平面內是否存在點
上的坐標平面內是否存在點![]() ,使以點
,使以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是矩形?若存在,請求出點
為頂點的四邊形是矩形?若存在,請求出點![]() 的坐標;若不存在,請說明理由。
的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 、
、![]() 兩組卡片共5張,
兩組卡片共5張,![]() 組中三張分別寫有數字2、4、6,
組中三張分別寫有數字2、4、6,![]() 組中兩張分別寫有數字3、5,它們除數字外其他都相同.
組中兩張分別寫有數字3、5,它們除數字外其他都相同.
(1)隨機從![]() 組中抽取一張,則抽到數字是2的概率為______;
組中抽取一張,則抽到數字是2的概率為______;
(2)分別隨機從![]() 組、
組、![]() 組中各抽取一張.現制定這樣一個游戲規則:若所抽取的兩個數字之積為3的倍數,則甲獲勝;否則乙獲勝.請問這樣的游戲規則對甲乙雙方公平嗎?為什么?請你用畫樹狀圖或列表的方法計算并說明理由.
組中各抽取一張.現制定這樣一個游戲規則:若所抽取的兩個數字之積為3的倍數,則甲獲勝;否則乙獲勝.請問這樣的游戲規則對甲乙雙方公平嗎?為什么?請你用畫樹狀圖或列表的方法計算并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,點M,N在同一個正比例函數圖象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個全等的等腰直角三角形,斜邊長為2,按如圖放置,其中一個三角形45°角的項點與另一個三角形的直角頂點A重合,若三角形ABC固定,當另一個三角形繞點A旋轉時,它的角邊和斜邊所在的直線分別與邊BC交于點E、F,設BF=![]() CE=
CE=![]() 則
則![]() 關于
關于![]() 的函數圖象大致是( )
的函數圖象大致是( )
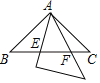
A.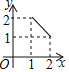 B.
B.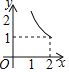 C.
C.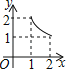 D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
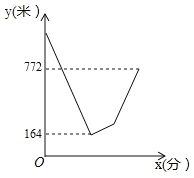
【題目】某個周末小月和小華在南濱路跑步鍛煉身體,兩人同時從A點出發,沿直線跑到B點后馬上掉頭原路返回A點算一個來回,回到A點后又馬上調頭去往B點,以此類推,每人要完成2個來回。一直兩人全程均保持勻速,掉頭時間忽略不計。如圖所示是小華從出發到他率先完成第一個來回為止,兩人到B點的距離之和y(米)與小華跑步時間x(分鐘)之間的函數圖像,則當小華跑完2個來回時,小月離B點的距離為___米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E為□ABCD中一點,EA=ED,∠AED=90,點F,G分別為AB,BC上的點,連接DF,AG,AD=AG=DF,且AG⊥DF于點H,連接EG,DG,延長AB,DG相交于點P.
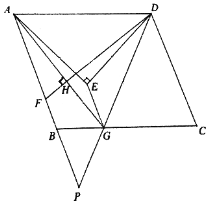
(1)若AH=6,FH=2,求AE的長;
(2)求證:∠P=45;
(3)若DG=2PG,求證:∠AGE=∠EDG.
查看答案和解析>>
科目:初中數學 來源: 題型:
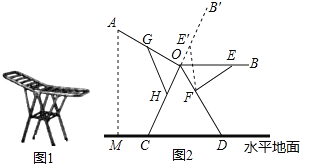
【題目】圖1是一種折疊式晾衣架.晾衣時,該晾衣架左右晾衣臂張開后示意圖如圖2所示,兩支腳OC=OD=10分米,展開角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.當∠AOC=90°時,點A離地面的距離AM為_______分米;當OB從水平狀態旋轉到OB′(在CO延長線上)時,點E繞點F隨之旋轉至OB′上的點E′處,則B′E′﹣BE為_________分米.
查看答案和解析>>
科目:初中數學 來源: 題型:
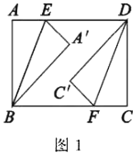
【題目】綜合與實踐:
動手操作:如圖1,四邊形![]() 是一張矩形紙片,
是一張矩形紙片,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 邊上,且
邊上,且![]() ,連接
,連接![]() ,
,![]() .將
.將![]() ,
,![]() 分別沿
分別沿![]() ,
,![]() 折疊,點
折疊,點![]() ,
,![]() 分別落在點
分別落在點![]() ,
,![]() 處.
處.
探究展示:
(1)“刻苦小組”發現:![]() ,且
,且![]() ,并展示了如下的證明過程.
,并展示了如下的證明過程.
證明:在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .(依據1)
.(依據1)
∴![]() .
.
∴![]() .(依據2)
.(依據2)
反思交流:①上述證明過程中的“依據1”與“依據2”分別指什么?
②“勤奮小組”認為:還可以通過證明四邊形![]() 是平行四邊形獲證,請你根據“勤奮小組”的證明思路寫出證明過程.
是平行四邊形獲證,請你根據“勤奮小組”的證明思路寫出證明過程.
猜想證明:
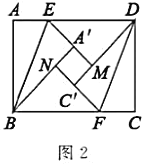
(2)如圖2,折疊過程中,當點![]() ,
,![]() 在直線
在直線![]() 的同側時,延長
的同側時,延長![]() 交
交![]() 于點
于點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,則四邊形
,則四邊形![]() 是什么特殊四邊形?請說明理由.
是什么特殊四邊形?請說明理由.
聯想拓廣:
(3)如圖3,連接![]() ,
,![]() ,
,![]() .
.

①當![]() 時,
時,![]() 的長為________;
的長為________;
②![]() 的長有最大值嗎?若有,請你直接寫出
的長有最大值嗎?若有,請你直接寫出![]() 長的最大值和此時四邊形
長的最大值和此時四邊形![]() 的形狀;若沒有,請說明理由.
的形狀;若沒有,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com