
如圖,⊙O的半徑r=25,四邊形ABCD內接圓⊙O,AC⊥BD于點H,P為CA延長線上的一點,且∠PDA=∠ABD.
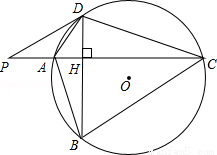
(1)試判斷PD與⊙O的位置關系,并說明理由;
(2)若tan∠ADB=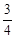 ,PA=
,PA=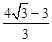 AH,求BD的長;
AH,求BD的長;
(3)在(2)的條件下,求四邊形ABCD的面積.
解:(1)PD與圓O相切。理由如下:
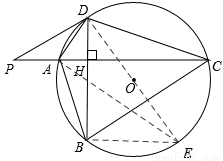
如圖,連接DO并延長交圓于點E,連接AE,
∵DE是直徑,∴∠DAE=90°。∴∠E+∠ADE=90°。
∵∠PDA=∠ABD=∠E,∴∠PDA+∠ADE=90°。
∴PD⊥DO。
∴PD與圓O相切于點D。
(2)∵tan∠ADB=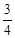 ,∴可設AH=3k,則DH=4k,
,∴可設AH=3k,則DH=4k,
∵PA=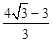 AH,∴PA=(
AH,∴PA=(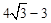 )k,
)k,
∴PH=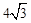 k。
k。
∴在Rt△PDH中,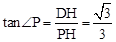 。∴∠P=30°,∠PDH=60°。
。∴∠P=30°,∠PDH=60°。
∵PD⊥DO,∴∠BDE=90°﹣∠PDH=30°。
連接BE,則∠DBE=90°,DE=2r=50,
∴BD=DE•cos30°=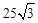 。
。
(3)由(2)知,BH=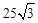 ﹣4k,∴HC=
﹣4k,∴HC=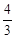 (
(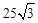 ﹣4k)。
﹣4k)。
又∵PD2=PA×PC,∴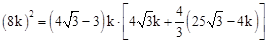 。
。
解得:k=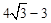 。
。
∴AC=3k+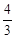 (
(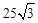 ﹣4k)=
﹣4k)=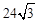 +7,
+7,
∴S四邊形ABCD=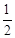 BD•AC=
BD•AC=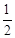 ×
×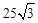 ×(
×(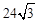 +7)=900+
+7)=900+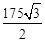 。
。
【解析】(1)首先連接DO并延長交圓于點E,連接AE,由DE是直徑,可得∠DAE的度數,又由∠PDA=∠ABD=∠E,可證得PD⊥DO,即可得PD與圓O相切于點D。
(2)由tan∠ADB=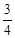 ,可設AH=3k,則DH=4k,又由PA=
,可設AH=3k,則DH=4k,又由PA=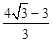 AH,易求得∠P=30°,∠PDH=60°,連接BE,則∠DBE=90°,DE=2r=50,可得BD=DE•cos30°=
AH,易求得∠P=30°,∠PDH=60°,連接BE,則∠DBE=90°,DE=2r=50,可得BD=DE•cos30°=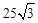 。
。
(3)由(2)易得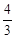 (
(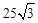 ﹣4k),又由PD2=PA×PC,可得方程:
﹣4k),又由PD2=PA×PC,可得方程: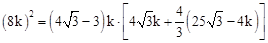 ,解此方程即可求得AC的長,繼而求得四邊形ABCD的面積。
,解此方程即可求得AC的長,繼而求得四邊形ABCD的面積。


科目:初中數學 來源: 題型:
 21、如圖,⊙O的半徑OD經過弦AB(不是直徑)的中點C,過AB的延長線上一點P作⊙O的切線PE,E為切點,PE∥OD;延長直徑AG交PE于點H;直線DG交OE于點F,交PE于點K.
21、如圖,⊙O的半徑OD經過弦AB(不是直徑)的中點C,過AB的延長線上一點P作⊙O的切線PE,E為切點,PE∥OD;延長直徑AG交PE于點H;直線DG交OE于點F,交PE于點K.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,⊙O的半徑為1,點P是⊙O上一點,弦AB垂直平分線段OP.點D是弦AB所對劣弧上的任一點(異于點A、B),過點D作DE⊥AB于點E,以點D為圓心,DE長為半徑作⊙D,連接AD、BD.分別過點A、B作⊙D的切線,兩條切線交于點C.下列結論:
如圖,⊙O的半徑為1,點P是⊙O上一點,弦AB垂直平分線段OP.點D是弦AB所對劣弧上的任一點(異于點A、B),過點D作DE⊥AB于點E,以點D為圓心,DE長為半徑作⊙D,連接AD、BD.分別過點A、B作⊙D的切線,兩條切線交于點C.下列結論:| 3 |
| S |
| DE2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,⊙O的半徑為3cm,B為⊙O外一點,OB交⊙O于點A,AB=OA,動點P從點A出發,以πcm/s的速度在⊙O上按逆時針方向運動一周回到點A立即停止.當點P運動的時間為( )s時,BP與⊙O相切.
如圖,⊙O的半徑為3cm,B為⊙O外一點,OB交⊙O于點A,AB=OA,動點P從點A出發,以πcm/s的速度在⊙O上按逆時針方向運動一周回到點A立即停止.當點P運動的時間為( )s時,BP與⊙O相切.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com