
【題目】到某實體店購買甲,乙兩種品牌的計算器,乙品牌的計算器比甲品牌的計算器單價高![]() 元;購買
元;購買![]() 個甲品牌計算器和
個甲品牌計算器和![]() 個乙品牌計算器共需要
個乙品牌計算器共需要![]() 元.
元.
(1)請計算該實體店甲,乙兩種品牌計算器的單價各是多少元?
(2)某網店也賣同樣品牌的計算器,單價和實體店相比:甲品牌計算器便宜![]() 元,乙品牌計算器
元,乙品牌計算器![]() 折出單.如果在該網店購買
折出單.如果在該網店購買![]() 個兩種品牌的計算器,總費用不超過
個兩種品牌的計算器,總費用不超過![]() 元,且保證乙品牌計算器不少于
元,且保證乙品牌計算器不少于![]() 個,請你設計出網購方案.
個,請你設計出網購方案.
【答案】(1)實體店甲種品牌計算器的單價為50元,,乙種單價為80元,(2)四種網購方案,見解析
【解析】
(1)設實體店甲種品牌計算器的單價為x元,,乙種為y元,根據題意列出二元一次方程組即可求解;
(2)設網店購買的甲品牌計算器為a個,則購買乙品牌計算器為(50-a)個,找到不等式列出不等式組即可求解.
(1)設實體店甲種品牌計算器的單價為x元,,乙種單價為y元,
根據題意得![]()
解得![]()
∴實體店甲種品牌計算器的單價為50元,,乙種單價為80元,
(2)設網店購買的甲品牌計算器為a個,則購買乙品牌計算器為(50-a)個,
依題意得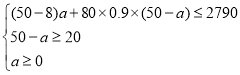
解得27≤a≤30
故有四種網購方案,分別是:①網店購買的甲品牌計算器為27個,則購買乙品牌計算器為23個;
②網店購買的甲品牌計算器為28個,則購買乙品牌計算器為22個;
③網店購買的甲品牌計算器為29個,則購買乙品牌計算器為31個;
④網店購買的甲品牌計算器為30個,則購買乙品牌計算器為20個;


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】某中學七年級開展演講比賽,學校決定購買一些筆記本和鋼筆作為獎品.現了解情況如下:甲、乙兩家商店出售兩種同樣品牌的筆記本和鋼筆.筆記本定價為每本20元,鋼筆每支定價5元,經洽談后,甲店每買一本筆記本贈一支鋼筆;乙店全部按定價的9折優惠.七年級需筆記本20本,鋼筆若干支(不小于20支).問:
(1)如果購買鋼筆![]() (
(![]() 不小于20)支,則在甲店購買需付款 ______ 元,在乙店購買需付款 _______________ 元.(用x的代數式表示)
不小于20)支,則在甲店購買需付款 ______ 元,在乙店購買需付款 _______________ 元.(用x的代數式表示)
(2)當購買鋼筆多少支時,在兩店購買付款一樣?
查看答案和解析>>
科目:初中數學 來源: 題型:
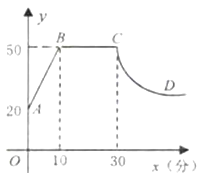
【題目】心理學研究發現,一般情況下,在一節45分鐘的課中,學生的注意力隨學習時間的變化而變化.開始學習時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指標數y隨時間x(分鐘)的變化規律如下圖所示(其中![]() 、
、![]() 分別為線段,
分別為線段,![]() 為雙曲線的一部分)。
為雙曲線的一部分)。
(1)開始學習后第5分鐘時與第35分鐘時相比較,何時學生的注意力更集中?
(2)某些數學內容的課堂學習大致可分為三個環節:即“教師引導,回顧舊知——自主探索,合作交流——總結歸納,鞏固提高”.其中重點環節“自主探索,合作交流”這一過程一般需要30分鐘才能完成,為了確保效果,要求學習時的注意力指標數不低于40,請問這樣的課堂學習安排是否合理?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】年是我市“創建國家衛生城市”第一年,為了了解本班![]() 名學生對“創衛”的知曉率,某同學采取隨機抽樣的方法進行問卷調查,調查分為四個選項:
名學生對“創衛”的知曉率,某同學采取隨機抽樣的方法進行問卷調查,調查分為四個選項:![]() 非常了解,
非常了解,![]() 比較了解,
比較了解,![]() 基本了解,
基本了解,![]() 不甚了解.數據整理如下:
不甚了解.數據整理如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
請畫出條形圖和扇形圖來描述以上統計數據.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小華和小明用兩張相同的長方形紙做數學實驗,先在兩條較長的邊上各取一點畫一條線,沿畫線剪開后再對齊,并將其中一部分沿長邊平移一定的距離, 陰影表示平移拉開的區域.小華畫了一條線段,如圖①所示;小明畫了一條曲線,如圖②所示.
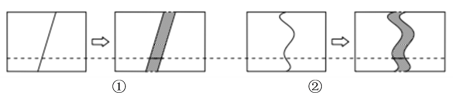
(1)設長方形的長為![]() ,寬為
,寬為![]() ,平移的距離為
,平移的距離為![]() ,請計算兩個陰影區域的面積,由計算結果你發現了什么?
,請計算兩個陰影區域的面積,由計算結果你發現了什么?
(2)任意畫一條與長邊平行的直線,被陰影部分所截得的線段是否相等?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小李某天的運營全是在東西走向的人民大街進行的,如果規定向東為正,向西為負,他這天下午的行車里程如下(單位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)將最后一名乘客送到目的地時,小李距下午出車地點的距離是多少?
(2)若汽車的耗油量為0.5L/㎞,那么這天下午汽車共耗油多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十一”期間,某風景區在7天中每天游客的人數變化如下表(正數表示比前一天多的人數,負數表示比前一天少的人數)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人數變化 單位:萬人 |
|
|
|
|
|
|
|
(1)若9月30日的游客人數記為![]() ,請用含
,請用含![]() 的代數式表示10月2日的游客人數?
的代數式表示10月2日的游客人數?
(2)請判斷七天內游客人數最多的是哪天?請說明理由.
(3)此風景區一方面給廣大市民提供一個休閑游玩的好去處;另一方面拉動了內需,促進了消費.若9月30日的游客人數為1萬人,進園的人每人平均消費60元,問“十一”期間所有游園人員在此風景區的總消費是多少元?(用科學記數法表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在透明紙面上有一數軸(如圖1),折疊透明紙面.
(1)若表示![]() 的點與表示
的點與表示![]() 的點重合,則表示
的點重合,則表示![]() 的點與表示_________的點重合;
的點與表示_________的點重合;
(2)若表示![]() 的點與表示
的點與表示![]() 的點重合,回答以下問題:
的點重合,回答以下問題:
①表示![]() 的點與表示__的點重合;
的點與表示__的點重合;
②如圖2,若數軸上![]() 、
、![]() 兩點之間的距離為
兩點之間的距離為![]() (點
(點![]() 在點
在點![]() 的左側),且
的左側),且![]() 、
、![]() 兩點經折疊后重合,則
兩點經折疊后重合,則![]() 、
、![]() 兩點表示的數分別是_________、_________.
兩點表示的數分別是_________、_________.
(3)如圖3,若![]() 和
和![]() 表示的點
表示的點![]() 和點
和點![]() 經折疊后重合
經折疊后重合![]() ,折痕與數軸的交點為折痕點.已知線段
,折痕與數軸的交點為折痕點.已知線段![]() 上兩點
上兩點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側,
的左側,![]() ),
),![]() .當線段
.當線段![]() 的端點與折痕點重合時,求
的端點與折痕點重合時,求![]() 、
、![]() 兩點表示的數分別是多少?(用含
兩點表示的數分別是多少?(用含![]() ,
,![]() ,
,![]() 的代數式表示).
的代數式表示).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com