
【題目】如圖,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于點D.點P從點A出發,以每秒1個單位長度的速度沿線段AB向終點B運動.在運動過程中,以點P為頂點作長為2,寬為1的矩形PQMN,其中PQ=2,PN=1,點Q在點P的左側,MN在PQ的下分,且PQ總保持與AC垂直.設P的運動時間為t(秒)(t>0),矩形PQMN與△ACD的重疊部分圖形面積為S(平方單位).
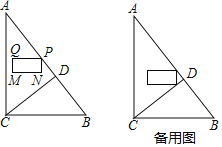
(1)求線段CD的長;
(2)當矩形PQMN與線段CD有公共點時,求t的取值范圍;
(3)當點P在線段AD上運動時,求S與t的函數關系式.
【答案】(1)CD=![]() ;(2)
;(2)![]() ≤t≤
≤t≤![]() ;(3)當0<t<
;(3)當0<t<![]() 時,S=
時,S=![]() ;當
;當![]() ≤t≤
≤t≤![]() 時, S=2;當
時, S=2;當![]() <t≤
<t≤![]() 時,S=
時,S=![]() .
.
【解析】
(1)由勾股定理得出AB=10,由△ABC的面積得出ACBC=ABCD,即可得出CD的長;
(2)分兩種情形:①當點N在線段CD上時,如圖1所示,利用相似三角形的性質求解即可.②當點Q在線段CD上時,如圖2所示,利用相似三角形的性質求解即可;
(3)首先求出點Q落在AC上的運動時間t,再分三種情形:①當0<t<![]() 時,重疊部分是矩形PNYH,如圖4所示,②當
時,重疊部分是矩形PNYH,如圖4所示,②當![]() ≤t≤
≤t≤![]() 時,重合部分是矩形PNMQ,S=PQPN=2,③當
時,重合部分是矩形PNMQ,S=PQPN=2,③當![]() <t≤
<t≤![]() 時,如圖5中重疊部分是五邊形PQMJI,分別求解即可.
時,如圖5中重疊部分是五邊形PQMJI,分別求解即可.
解:(1)∵∠ACB=90°,AC=8,BC=6,
∴AB=![]() =10,
=10,
∵S△ABC=![]() ACBC=
ACBC=![]() ABCD,
ABCD,
∴ACBC=ABCD,即:8×6=10×CD,
∴CD=![]() ;
;
(2)在Rt△ADC中,AD=![]() ,BD=ABAD=
,BD=ABAD=![]() ,
,
當點N在線段CD上時,如圖1所示:
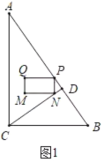
∵矩形PQMN,PQ總保持與AC垂直,
∴PN∥AC,
∴∠NPD=∠CAD,
∵∠PDN=∠ADC,
∴△PDN∽△ADC,
∴![]() ,即:
,即: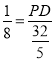 ,
,
解得:PD=![]() ,
,
∴t=ADPD=![]() ;
;
當點Q在線段CD上時,如圖2所示:

∵PQ總保持與AC垂直,
∴PQ∥BC,△DPQ∽△DBC,
∴![]() ,即:
,即: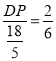 ,
,
解得:DP=![]() ,
,
∴t=AD+DP=![]() ,
,
∴當矩形PQMN與線段CD有公共點時,t的取值范圍為:![]() ≤t≤
≤t≤![]() ;
;
(3)當Q在AC上時,如圖3所示:
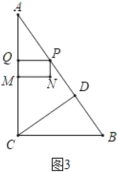
∵PQ總保持與AC垂直,
∴PQ∥BC,△APQ∽△ABC,
∴![]() ,即:
,即:![]() ,
,
解得:AP=![]() ,
,
當0<t<![]() 時,重疊部分是矩形PNYH,如圖4所示:
時,重疊部分是矩形PNYH,如圖4所示:
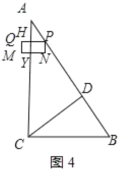
∵PQ∥BC,
∴△APH∽△ABC,
∴![]() ,即:
,即:![]() ,
,
∴PH=![]() ,
,
∴S=PHPN=![]() ;
;
當![]() ≤t≤
≤t≤![]() 時,重合部分是矩形PNMQ,S=PQPN=2;
時,重合部分是矩形PNMQ,S=PQPN=2;
當![]() <t≤
<t≤![]() 時,如圖5中重疊部分是五邊形PQMJI,
時,如圖5中重疊部分是五邊形PQMJI,
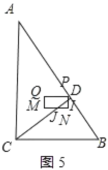
易得△PDI∽△ACB∽△JNI,
∴![]() ,即:
,即: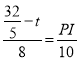 ,
,
∴PI=(![]() t)
t)![]() ,
,
∴![]() ,即:
,即: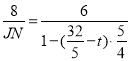 ,
,
∴JN=![]() ,
,
S=S矩形PNMQS△JIN=2![]() ·(
·(![]() )·[1(
)·[1(![]() t)
t)![]() ]=
]=![]() .
.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:初中數學 來源: 題型:
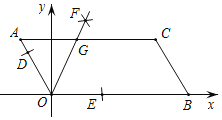
【題目】如圖,已知AOBC的頂點O(0,0),A(﹣1,2),點B在x軸正半軸上按以下步驟作圖:①以點O為圓心,適當長度為半徑作弧,分別交邊OA,OB于點D,E;②分別以點D,E為圓心,大于![]() DE的長為半徑作弧,兩弧在∠AOB內交于點F;③作射線OF,交邊AC于點G,則點G的坐標為( )
DE的長為半徑作弧,兩弧在∠AOB內交于點F;③作射線OF,交邊AC于點G,則點G的坐標為( )
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個水果市場某品種蘋果的銷售方式如下表:
購買蘋數量(千克) | 不超過 | 超過 |
每千克的價格(元) |
|
|
(1)如果小明購買![]() 千克的蘋果,那么他需要付___________元.
千克的蘋果,那么他需要付___________元.
(2)小明分兩次共購買![]() 千克的蘋果,第二次購買的數量多于第一次購買的數量,若他兩次共付
千克的蘋果,第二次購買的數量多于第一次購買的數量,若他兩次共付![]() 元,求他兩次分別購買蘋果的數量.
元,求他兩次分別購買蘋果的數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著粵港澳大灣區建設的加速推進,廣東省正加速布局以5G等為代表的戰略性新興產業,據統計,目前廣東5G基站的數量約1.5萬座,計劃到2020年底,全省5G基站數是目前的4倍,到2022年底,全省5G基站數量將達到17.34萬座。
(1)計劃到2020年底,全省5G基站的數量是多少萬座?;
(2)按照計劃,求2020年底到2022年底,全省5G基站數量的年平均增長率。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點![]() 為直線
為直線![]() 上一點,過點
上一點,過點![]() 作射線
作射線![]() ,使
,使![]() 將一直角三角板的直角頂點放在點
將一直角三角板的直角頂點放在點![]() 處,一邊
處,一邊![]() 在射線
在射線![]() 上,另一邊
上,另一邊![]() 在直線
在直線![]() 的下方.
的下方.
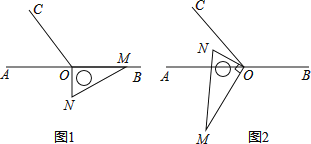
(1)將圖1中的三角板繞點![]() 按每秒
按每秒![]() 的速度沿順時針方向旋轉,使
的速度沿順時針方向旋轉,使![]() 落在
落在![]() 上.在旋轉的過程中,假如第
上.在旋轉的過程中,假如第![]() 秒時,
秒時,![]() 、
、![]() 、
、![]() 三條射線構成的角中有兩個角相等,求此時
三條射線構成的角中有兩個角相等,求此時![]() 的值為多少?
的值為多少?
(2)將圖1中的三角板繞點![]() 順時針旋轉(如圖2),使
順時針旋轉(如圖2),使![]() 在
在![]() 的內部,請探究:
的內部,請探究:![]() 與
與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】無錫某學校準備組織學生及學生家長到南京大學參觀體驗,為了便于管理,所有人員到南京必須乘坐在同一列動車上;根據報名人數,若都買一等座單程火車票需5032元,若都買二等座單程火車票且花錢最少,則需2970元;已知學生家長人數是教師人數的2倍,無錫到南京的動車票價格(動車學生票只有二等座可以打6折)如下表所示:
運行區間 | 票價 | ||
上車站 | 下車站 | 一等座 | 二等座 |
無錫 | 南京 | 68(元) | 55(元) |
(1)參加參觀體驗的老師、家長與學生各有多少人?
(2)由于各種原因,二等座火車票單程只能買x張(x小于參加體驗的人數),其余的需買一等座火車票,在保證每位參與人員都有座位坐的前提下,請你設計最經濟的購票方案,并寫出購買火車票的總費用(單程)y與x之間的函數關系式.
(3)請你做一個預算,按第(2)小題中的購票方案,購買單程火車票的總費用至少是多少錢?最多是多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
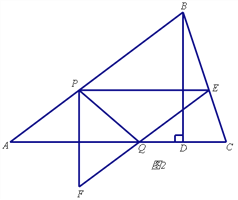
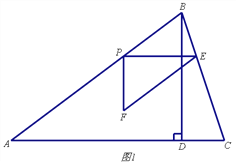
【題目】如圖1,在銳角△ABC中,AB=5,tanC=3,BD⊥AC于點D,BD=3,點P從點A出發,以每秒1個單位長度的速度沿AB向終點B運動,過點P作PE∥AC交邊BC于點E,以PE為邊作Rt△PEF,使∠EPF=90°,點F在點P的下方,且EF∥AB.設△PEF與△ABD重疊部分圖形的面積為S(平方單位)(S>0),點P的運動時間為t(秒)
(t>0).
(1)求線段AC的長.
(2)當△PEF與△ABD重疊部分圖形為四邊形時,求S與t之間的函數關系式,并寫出t的取值范圍.
(3)若邊EF所在直線與邊AC交于點Q,連結PQ,如圖2,直接寫出△ABC的某一頂點到P、Q兩點距離相等時t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在三角形ABC中,∠A=90°,AB=AC=2,將△ABC折疊,使點B落在邊AC上點D (不與點A重合)處,折痕為PQ,當重疊部分△PQD為等腰三角形時,則AD的長為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com