
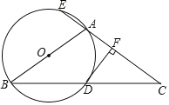
【題目】如圖,△ABC中,AB=AC,以AB為直徑的⊙O與BC相交于點D,與CA的延長線相交于點E,過點D作DF⊥AC于點F.
(1)試說明DF是⊙O的切線;
(2)若AC=3AE=6,求tanC
【答案】(1)見解析(2)![]()
【解析】
(1)連接OD,根據等邊對等角得出∠B=∠ODB,∠B=∠C,得出∠ODB=∠C,證得OD∥AC,證得OD⊥DF,從而證得DF是⊙O的切線;
(2)由AC=3AE可得AB=AC=3AE,EC=4AE;連結BE,由AB是直徑可知∠AEB=90°,根據勾股定理求出BE,解直角三角形求出即可.
(1)連接OD,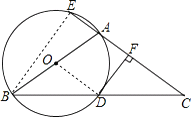
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,點D在⊙O上,
∴DF是⊙O的切線;
(2)連接BE,
∵AB是直徑,
∴∠AEB=90°,
∵AB=AC,AC=3AE,
∴AB=3AE,CE=4AE,
∴BE=![]() =2
=2![]() AE
AE
在Rt△BEC中,tanC=![]()


科目:初中數學 來源: 題型:
【題目】為落實素質教育要求,促進學生全面發展,我市某中學2014年投資11萬元新增一批電腦,計劃以后每年以相同的增長率進行投資,2016年投資18.59萬元.
(1)求該學校為新增電腦投資的年平均增長率;
(2)從2014年到2016年,該中學三年為新增電腦共投資多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
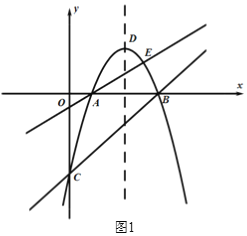
【題目】如圖1,拋物線![]() 與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線AE:
與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線AE:![]() 與拋物線相交于另一點E,點D為拋物線的頂點.
與拋物線相交于另一點E,點D為拋物線的頂點.
(1)求直線BC的解析式及點E的坐標;
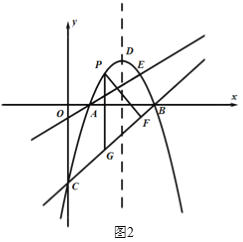
(2)如圖2,直線AE上方的拋物線上有一點P,過點P作PF⊥BC于點F,過點P作平行于![]() 軸的直線交直線BC于點G,當△PFG周長最大時,在
軸的直線交直線BC于點G,當△PFG周長最大時,在![]() 軸上找一點M,在AE上找一點N,使得
軸上找一點M,在AE上找一點N,使得![]() 值最小,請求出此時N點的坐標及
值最小,請求出此時N點的坐標及![]() 的最小值;
的最小值;
(3)在第(2)問的條件下,點R為拋物線對稱軸上的一點,在平面直角坐標系中是否存在點S,使以點N,E,R,S為頂點的四邊形為矩形,若存在,請直接寫出點S的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與坐標軸分別交于點A、B,與直線
與坐標軸分別交于點A、B,與直線![]() 交于點C.在線段OA上,動點Q以每秒1個單位長度的速度從點O出發向點A做勻速運動,同時動點P從點A出發向點O做勻速運動,當點P、Q其中一點停止運動時,另一點也停止運動.分別過點P、Q作x軸的垂線,交直線AB、OC于點E、F,連接EF.若運動時間為t秒,在運動過程中四邊形PEFQ總為矩形(點P、Q重合除外)。
交于點C.在線段OA上,動點Q以每秒1個單位長度的速度從點O出發向點A做勻速運動,同時動點P從點A出發向點O做勻速運動,當點P、Q其中一點停止運動時,另一點也停止運動.分別過點P、Q作x軸的垂線,交直線AB、OC于點E、F,連接EF.若運動時間為t秒,在運動過程中四邊形PEFQ總為矩形(點P、Q重合除外)。
(1)求點P運動的速度是多少?
(2)當t為多少秒時,矩形PEFQ為正方形?
(3)當t為多少秒時,矩形PEFQ的面積S最大?并求出最大值。


查看答案和解析>>
科目:初中數學 來源: 題型:
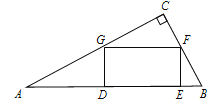
【題目】如圖,在Rt△ABC中,∠C=90°,矩形DEFG的頂點G、F分別在AC、BC上,DE在AB上.
(1)求證:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,直線
,直線![]() 是足球場的底線,
是足球場的底線,![]() 是球門,
是球門,![]() 點是射門點,連接
點是射門點,連接![]() ,
,![]() 叫做射門角.
叫做射門角.
(1)如圖![]() ,點
,點![]() 是射門點,另一射門點
是射門點,另一射門點![]() 在過
在過![]() 三點的圓外(未超過底線
三點的圓外(未超過底線![]() ).證明:
).證明:![]()
(2)如圖![]() ,
,![]() 經過球門端點
經過球門端點![]() ,直線
,直線![]() ,垂足為
,垂足為![]() 且與
且與![]() 相切與點
相切與點![]() ,
,![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() ,求此時一球員帶球沿直線
,求此時一球員帶球沿直線![]() 向底線方向運球時最大射門角的度數.
向底線方向運球時最大射門角的度數.
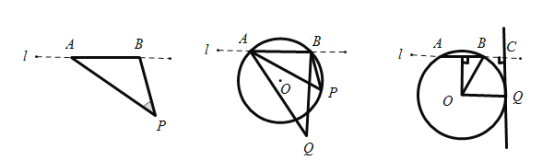
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于點P,點P在第一象限.PA⊥x軸于點A,PB⊥y軸于點B.一次函數的圖象分別交
的圖象交于點P,點P在第一象限.PA⊥x軸于點A,PB⊥y軸于點B.一次函數的圖象分別交![]() 軸、
軸、![]() 軸于點C、D,且S△PBD=4,
軸于點C、D,且S△PBD=4, ![]() .
.

(1)求點D的坐標;
(2)求一次函數與反比例函數的解析式;
(3)根據圖象寫出當![]() 時,一次函數的值大于反比例函數的值的
時,一次函數的值大于反比例函數的值的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),已知點G在正方形ABCD的對角線AC上,GE⊥BC,垂足為點E,GF⊥CD,垂足為點F.
(1)證明與推斷:
①求證:四邊形CEGF是正方形;
②推斷:![]() 的值為 :
的值為 :
(2)探究與證明:
將正方形CEGF繞點C順時針方向旋轉α角(0°<α<45°),如圖(2)所示,試探究線段AG與BE之間的數量關系,并說明理由:
(3)拓展與運用:
正方形CEGF在旋轉過程中,當B,E,F三點在一條直線上時,如圖(3)所示,延長CG交AD于點H.若AG=6,GH=2![]() ,則BC= .
,則BC= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】基本事實:“若ab=0,則a=0或b=0”.一元二次方程x2-x-2=0可通過因式分解化為(x-2)(x+1)=0,由基本事實得x-2=0或x+1=0,即方程的解為x=2或x=-1.
(1)、試利用上述基本事實,解方程:2x2-x=0:
(2)、若(x2+y2)(x2+y2-1)-2=0,求x2+y2的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com