Question

2．如圖，△ABC中，∠C=90°，AB=10cm，BC=6cm，若動點P從點C開始，按C→A→B→C的路徑運動，且速度為每秒1cm，設出發的時間為t秒．
（1）出發2秒后，求△ABP的周長．
（2）當t為幾秒時，BP平分∠ABC？
（3）問t為何值時，△BCP為等腰三角形？
（4）另有一點Q，從點C開始，按C→B→A→C的路徑運動，且速度為每秒2cm，若P、Q兩點同時出發，當P、Q中有一點到達終點時，另一點也停止運動．當t為何值時，直線PQ把△ABC的周長分成相等的兩部分？

Answer 1

分析 （1）由勾股定理求出AC=8 cm，動點P從點C開始，出發2秒后，則CP=2 cm，AP=6 cm，由勾股定理求出PB，即可得出結果；
（2）過點P作PD⊥AB于點D，由HL證明Rt△APD≌Rt△APC，得出AD=AC=6cm，因此BD=10-6=4cm，設PC=x cm，則PB=（8-x）cm，由勾股定理得出方程，解方程即可；
（3）分兩種情況：①若P在邊AC上時，BC=CP=6cm，此時用的時間為6s；
②若P在AB邊上時，有三種情況：
i若使BP=CB=6cm，此時AP=4cm，P運動的路程為4+8=12cm，用的時間為12時；          
ii）若CP=BC=6cm，過C作CD⊥AB于點D，根據面積法求得高CD=4.8cm，求出BP=2PD=7.2cm，得出P運動的路程為18-7.2=10.8cm，即可得出結果；       
ⅲ）若BP=CP，則∠PCB=∠B，證出PA=PC得出PA=PB=5cm，得出P的路程為13cm，即可得出結果；
（4）分兩種情況：①當P、Q沒相遇前：如圖6，P點走過的路程為t，Q走過的路程為2t，根據題意得出方程，解方程即可；
②當P、Q沒相遇后：當P點在AB上，Q在AC上，則AP=t-8，AQ=2t-16，根據題意得出方程，解方程即可；即可得出結果．

解答 解：（1）如圖1，由∠C=90°，AB=10cm，BC=6cm，
∴AC=8 cm，
∵動點P從點C開始，按C→A→B→C的路徑運動，且速度為每秒1cm，
∴出發2秒后，則CP=2 cm，AP=6 cm，
∵∠C=90°，
∴由勾股定理得PB=$\sqrt{P{C^2}+B{C^2}}$=$2\sqrt{10}cm$，
∴△ABP的周長為：AP+PB+AB=（16+$2\sqrt{10}$） cm．      
（2）如圖2所示，過點P作PD⊥AB于點D，
∵AP平分∠CAB，
∴PD=PC．                                
在Rt△APD與Rt△APC中，
$\left\{\begin{array}{l}{PD=PC}\\{AP=AP}\end{array}\right.$，
∴Rt△APD≌Rt△APC（HL），
∴AD=AC=6 cm，
∴BD=10-6=4 cm．                            
設PC=x cm，則PB=（8-x）cm
在Rt△BPD中，PD²+BD²=PB²，
即x²+4²=（8-x）²，
解得：x=3，
∴當t=3秒時，AP平分∠CAB；                     
（3）①如圖3，若P在邊AC上時，BC=CP=6cm，
此時用的時間為6s，△BCP為等腰三角形          
②若P在AB邊上時，有三種情況：
i）如圖4，若使BP=CB=6cm，此時AP=4cm，P運動的路程為4+8=12cm，
所以用的時間為12s時，△BCP為等腰三角形；          
ii）如圖5，若CP=BC=6cm，
過C作CD⊥AB于點D，根據面積法得：高CD=4.8cm，
在Rt△PCD中，PD=3.6cm，∴BP=2PD=7.2cm，
∴P運動的路程為18-7.2=10.8cm，
∴用的時間為10.8s時，△BCP為等腰三角形；          
ⅲ）如圖6，若BP=CP，則∠PCB=∠B，
∵∠ACP+∠BCP=90°，∠B+∠A=90°，
∴∠ACP=∠A，
∴PA=PC
∴PA=PB=5cm
∴P的路程為13cm，所以時間為13s時，△BCP為等腰三角形．   
綜上所述，當t為6s或12s或10.8s或13s時，△BCP為等腰三角形；
（3）分兩種情況：①當P、Q沒相遇前：如圖7，
P點走過的路程為tcm，Q走過的路程為2tcm，
∵直線PQ把△ABC的周長分成相等的兩部分，
∴t+2t=12，
∴t=4s；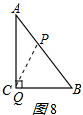                                          
②當P、Q沒相遇后：如圖8，
當P點在AB上，Q在AC上，則AP=t-8，AQ=2t-16，
∵直線PQ把△ABC的周長分成相等的兩部分，
∴t-8+2t-16=12，
∴t=12s，
∴當t為4秒或12秒時，直線PQ把△ABC的周長分成相等的兩部分．

點評 本題考查了全等三角形的判定與性質、等腰三角形的判定與性質、勾股定理、三角形面積的計算；本題綜合性強，熟練掌握等腰三角形的判定與性質，進行分類討論是解決問題的關鍵．