
【題目】如圖,在矩形ABCD中,AB═2,AD=![]() ,P是BC邊上的一點,且BP=2CP.
,P是BC邊上的一點,且BP=2CP.
(1)用尺規在圖①中作出CD邊上的中點E,連接AE、BE(保留作圖痕跡,不寫作法);
(2)如圖②,在(1)的條體下,判斷EB是否平分∠AEC,并說明理由;
(3)如圖③,在(2)的條件下,連接EP并廷長交AB的廷長線于點F,連接AP,不添加輔助線,△PFB能否由都經過P點的兩次變換與△PAE組成一個等腰三角形?如果能,說明理由,并寫出兩種方法(指出對稱軸、旋轉中心、旋轉方向和平移距離)
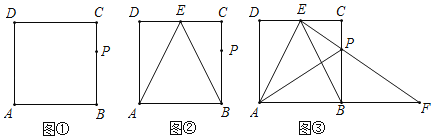
【答案】(1)作圖見解析;(2)EB是平分∠AEC,理由見解析; (3)△PFB能由都經過P點的兩次變換與△PAE組成一個等腰三角形,變換的方法為:將△BPF繞點B順時針旋轉120°和△EPA重合,①沿PF折疊,②沿AE折疊.
【解析】(1)根據作線段的垂直平分線的方法作圖即可得出結論;
(2)先求出DE=CE=1,進而判斷出△ADE≌△BCE,得出∠AED=∠BEC,再用銳角三角函數求出∠AED,即可得出結論;
(3)先判斷出△AEP≌△FBP,即可得出結論.
(1)依題意作出圖形如圖①所示;
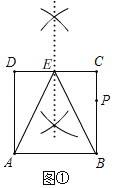
(2)EB是平分∠AEC,理由:
∵四邊形ABCD是矩形,
∴∠C=∠D=90°,CD=AB=2,BC=AD=![]() ,
,
∵點E是CD的中點,
∴DE=CE=![]() CD=1,
CD=1,
在△ADE和△BCE中,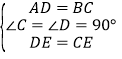 ,
,
∴△ADE≌△BCE,
∴∠AED=∠BEC,
在Rt△ADE中,AD=![]() ,DE=1,
,DE=1,
∴tan∠AED=![]() =
=![]() ,
,
∴∠AED=60°,
∴∠BCE=∠AED=60°,
∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,
∴BE平分∠AEC;
(3)∵BP=2CP,BC=![]() =
=![]() ,
,
∴CP=![]() ,BP=
,BP=![]() ,
,
在Rt△CEP中,tan∠CEP=![]() =
=![]() ,
,
∴∠CEP=30°,
∴∠BEP=30°,
∴∠AEP=90°,
∵CD∥AB,
∴∠F=∠CEP=30°,
在Rt△ABP中,tan∠BAP=![]() =
=![]() ,
,
∴∠PAB=30°,
∴∠EAP=30°=∠F=∠PAB,
∵CB⊥AF,
∴AP=FP,
∴△AEP≌△FBP,
∴△PFB能由都經過P點的兩次變換與△PAE組成一個等腰三角形,
變換的方法為:將△BPF繞點B順時針旋轉120°和△EPA重合,①沿PF折疊,②沿AE折疊.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,王老師將某班近三個月跳躍類項目的訓練情況做了統計,并繪制了折線統計圖,則根據圖中信息以下判斷錯誤的是( )
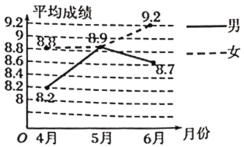
A.男女生5月份的平均成績一樣
B.4月到6月,女生平均成績一直在進步
C.4月到5月,女生平均成績的增長率約為![]()
D.5月到6月女生平均成績比4月到5月的平均成績增長快
查看答案和解析>>
科目:初中數學 來源: 題型:
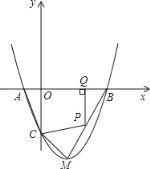
【題目】如圖,拋物線y=ax2+bx+c與x軸交于A、B兩點(點A在點B左側),與y軸交于點C,且當x=0和x=2時,y的值相等.直線y=3x﹣7與這條拋物線相交于兩點,其中一點的橫坐標是4,另一點是這條拋物線的頂點M.
(1)求這條拋物線的解析式;
(2)P為線段BM上一點,過點P向x軸引垂線,垂足為Q.若點P在線段BM上運動(點P不與點B、M重合),設OQ的長為t,四邊形PQAC的面積為S.求S與t之間的函數關系式及自變量t的取值范圍;
(3)在線段BM上是否存在點N,使△NMC為等腰三角形?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
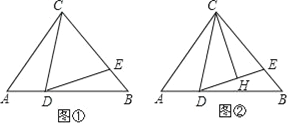
【題目】如圖在等腰三角形△ABC中,AC=BC,D、E分別為AB、BC上一點,∠CDE=∠A.
(1)如圖①,若BC=BD,求證:CD=DE;
(2)如圖②,過點C作CH⊥DE,垂足為H,若CD=BD,EH=1,求DE﹣BE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(―3,6)、B(―9,一3),以原點O為位似中心,相似比為![]() ,把△ABO縮小,則點A的對應點A′的坐標是( )
,把△ABO縮小,則點A的對應點A′的坐標是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段BD上一動點,分別過點B、D作AB⊥BD,ED⊥BD,連接AC、EC.已知AB=2,DE=1,BD=8,設CD=x.
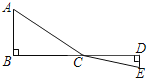
(1)用含x的代數式表示AC+CE的長;
(2)請問點C滿足什么條件時,AC+CE的值最小;
(3)根據(2)中的規律和結論,請構圖求出代數式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
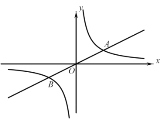
【題目】已知點A(2,1)是正比例函數ykx(其中k0)和反比例函數y![]() (其中t0)的圖像在第一象限的交點,點B是這兩個函數圖像的另一個交點,點C是x軸上一點.
(其中t0)的圖像在第一象限的交點,點B是這兩個函數圖像的另一個交點,點C是x軸上一點.
(1)求這兩個函數的解析式并直接寫出點B的坐標;
(2)求當ABC為等腰三角形時,點C的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com