
【題目】如圖,四邊形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,則四邊形ABCD的面積為( )
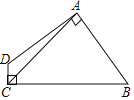
A. 15 B. 12.5 C. 14.5 D. 17
【答案】B
【解析】過A作AE⊥AC,交CB的延長線于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四邊形ABCD的面積與△ACE的面積相等,根據S△ACE=![]() ×5×5=12.5,即可得出結論.
×5×5=12.5,即可得出結論.
如圖,過A作AE⊥AC,交CB的延長線于E,
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB,
∴AC=AE,即△ACE是等腰直角三角形,
∴四邊形ABCD的面積與△ACE的面積相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四邊形ABCD的面積為12.5,
故選B.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:初中數學 來源: 題型:
【題目】如圖1,將長為10的線段OA繞點O旋轉90°得到OB,點A的運動軌跡為![]() ,P是半徑OB上一動點,Q是
,P是半徑OB上一動點,Q是![]() 上的一動點,連接PQ.
上的一動點,連接PQ.
發現:∠POQ=________時,PQ有最大值,最大值為________;
思考:(1)如圖2,若P是OB中點,且QP⊥OB于點P,求![]() 的長;
的長;
(2)如圖3,將扇形AOB沿折痕AP折疊,使點B的對應點B′恰好落在OA的延長線上,求陰影部分面積;
探究:如圖4,將扇形OAB沿PQ折疊,使折疊后的弧QB′恰好與半徑OA相切,切點為C,若OP=6,求點O到折痕PQ的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
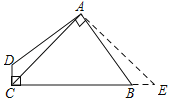
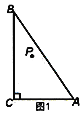
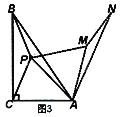
【題目】如圖1.在△ABC中,∠ACB=90°,點P為△ABC內一點.
(1)連接PB、PC,將△BCP沿射線CA方向平移,得到△DAE,點B、C、P的對應點分別為點D、A、E,連接CE.
①依題意,請在圖2中補全圖形;
②如果BP⊥CE,AB+BP=9,CE=![]() ,求AB的長.
,求AB的長.
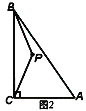
(2)如圖3,以點A為旋轉中心,將△ABP順時針旋轉60°得到△AMN,連接PA、PB、PC,當AC=4,AB=8時,根據此圖求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在直角坐標系中,
(1)請寫出△ABC各點的坐標.
(2)求出△ABC的面積.
(3)若把△ABC向上平移2個單位,再向右平移2個單位得△A′B′C′,在圖中畫出△ABC變化位置。

查看答案和解析>>
科目:初中數學 來源: 題型:
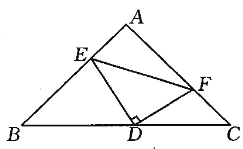
【題目】如圖,在等腰直角△ABC中,AB=AC,點D是斜邊BC的中點,點E、F分別是AB、AC邊上的點,且DE⊥DF.
(1)證明:BE+CF=EF2;
(2)若BE=12,CF=5,求△DEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
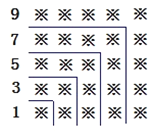
【題目】“數形結合"是一種重要的數學思想,觀察下面的圖形和算式.
![]()
![]()
![]()
![]()
解答下列問題:
(1)試猜想1+3+5+7+9+…+19=______=( );
(2)試猜想,當n是正整數時,1+3+5+7+9+…+(2n-1)= ;
(3)請用(2)中得到的規律計算:19+21+23+25+27+…+99.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等邊△ABC的邊長是2,以BC邊上的高AB1為邊作等邊三角形,得到第一個等邊△AB1C1;再以等邊△AB1C1的B1C1邊上的高AB2為邊作等邊三角形,得到第二個等邊△AB2C2;再以等邊△AB2C2的B2C2邊上的高AB3為邊作等邊三角形,得到第三個等邊△AB3C3;…,記△B1CB2的面積為S1,△B2C1B3的面積為S2,△B3C2B4的面積為S3,如此下去,則Sn=_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 為線段
為線段![]() 上一動點,分別過點
上一動點,分別過點![]() 作
作![]() ,
,![]() ,連接
,連接![]() .已知
.已知![]() ,設
,設![]() .
.
(1)用含![]() 的代數式表示
的代數式表示![]() 的值;
的值;
(2)探究:當點![]() 滿足什么條件時,
滿足什么條件時,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根據(2)中的結論,請構造圖形求代數式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 城有肥料200噸,
城有肥料200噸,![]() 城有肥料300噸.現將這些肥料全部運往
城有肥料300噸.現將這些肥料全部運往![]() ,
,![]() 兩鄉.
兩鄉. ![]() 鄉需要的肥料比
鄉需要的肥料比![]() 鄉少20噸.從
鄉少20噸.從![]() 城運往
城運往![]() ,
,![]() 兩鄉的費用分別為每噸20元和25元;從
兩鄉的費用分別為每噸20元和25元;從![]() 城運往
城運往![]() ,
,![]() 兩鄉的費用分別為每噸15元和24元.
兩鄉的費用分別為每噸15元和24元.
(1)求![]() ,
,![]() 兩鄉各需肥料多少噸?
兩鄉各需肥料多少噸?
(2)設從![]() 城運往
城運往![]() 鄉的肥料為
鄉的肥料為![]() 噸,全部肥料運往
噸,全部肥料運往![]() ,
,![]() 兩鄉的總運費為
兩鄉的總運費為![]() 元,求
元,求![]() 與
與![]() 之間的函數關系式,并直接寫出自變量
之間的函數關系式,并直接寫出自變量![]() 的取值范圍;
的取值范圍;
(3)因近期持續暴雨天氣,為安全起見,從![]() 城到
城到![]() 鄉需要繞道運輸,實際運費每噸增加了
鄉需要繞道運輸,實際運費每噸增加了![]() 元(
元(![]() ),其它路線運費不變.此時全部肥料運往
),其它路線運費不變.此時全部肥料運往![]() ,
,![]() 兩鄉所需最少費用為10520元,則
兩鄉所需最少費用為10520元,則![]() 的值為__ (直接寫出結果).
的值為__ (直接寫出結果).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com