
分析 (1)由月銷售利潤=每千克的利潤×可賣出千克數,把相關數值代入即可;
(2)根據“月銷售利潤為8000元”列出一元二次方程,解之可得答案;
(3)將函數解析式配方成頂點式可得二次函數的最值.
解答 解:(1)可賣出千克數為500-10(x-50)=1000-10x,
y與x的函數表達式為y=(x-40)(1000-10x)=-10x2+1400x-40000;
(2)根據題意得-10x2+1400x-40000=8000,
解得:x=60或x=80,
答:當售價定為60元或80元時,該商店月銷售利潤為8000元;
(3)∵y=(x-40)[500-10(x-50)]=-10x2+1400x-40000=-10(x-70)2+9000,
∴當x=70時,利潤最大為9000元.
答:當售價為70元,利潤最大,最大利潤是9000元.
點評 本題主要考查了二次函數的應用及解一元二次方程的能力,能正確表示出月銷售量是解題的關鍵.求二次函數的最大(小)值有三種方法,第一種可由圖象直接得出,第二種是配方法,第三種是公式法,常用的是后兩種方法.


科目:初中數學 來源: 題型:填空題
 定義:如圖,點M,N把線段AB分割成三條線段AM,MN和BN,若以AM,MN,BN為邊的三角形是一個直角三角形,則稱點M,N是線段AB的勾股分割點.若AM=2,MN=3,則BN的長為$\sqrt{3}$或$\sqrt{15}$.
定義:如圖,點M,N把線段AB分割成三條線段AM,MN和BN,若以AM,MN,BN為邊的三角形是一個直角三角形,則稱點M,N是線段AB的勾股分割點.若AM=2,MN=3,則BN的長為$\sqrt{3}$或$\sqrt{15}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
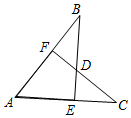 如圖,AB=AC,CF⊥AB于F,BE⊥AC于E,CF與BE交于點D.有下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③點D在∠BAC的平分線上.以上結論正確的有①②③.
如圖,AB=AC,CF⊥AB于F,BE⊥AC于E,CF與BE交于點D.有下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③點D在∠BAC的平分線上.以上結論正確的有①②③.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com