
【題目】如圖,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.點P從A點出發沿A→C→B路徑向終點運動,終點為B點;點Q從B點出發沿B→C→A路徑向終點運動,終點為A點.點P和Q分別以每秒1cm和3cm的運動速度同時開始運動,當一個點到達終點時另一個點也停止運動,在某時刻,分別過P和Q作PE⊥l于E,QF⊥l于F.設運動時間為t秒,則當t=______秒時,△PEC與△QFC全等.

【答案】1或![]() 或12.
或12.
【解析】
根據題意進行分類討論,根據全等三角形的性質得出CP=CQ,代入得出關于t的方程,求出即可.
①如圖1,P在AC上,Q在BC上,
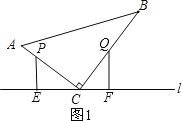
∵PE⊥l,QF⊥l,
∴∠PEC=∠QFC=90°,
∵∠ACB=90°,
∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,
∴∠EPC=∠QCF,
則△PCE≌△CQF,
∴PC=CQ,
即6-t=8-3t,
t=1;
②如圖2,P在BC上,Q在AC上,
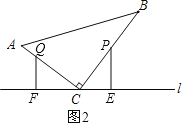
∵由①知:PC=CQ,
∴t-6=3t-8,
t=1;
t-6<0,即此種情況不符合題意;
③當P、Q都在AC上時,如圖3,
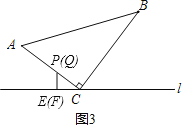
CP=6-t=3t-8,
t=![]() ;
;
④當Q到A點停止,P在BC上時,AC=PC,t-6=6時,解得t=12.
∵P的速度是每秒1cm,Q的速度是每秒3cm,
P和Q都在BC上的情況不存在.
故答案為:1或![]() 或12.
或12.


 每課必練系列答案
每課必練系列答案科目:初中數學 來源: 題型:
【題目】為了了解全校1500名學生對學校設置的籃球、羽毛球、乒乓球、踢毽子、跳繩共5項體育活動的喜愛情況,在全校范圍內隨機抽查部分學生,對他們喜愛的體育項目(每人只選一項)進行了問卷調查,將統計數據繪制成如圖兩幅不完整統計圖,請根據圖中提供的信息解答下列各題.
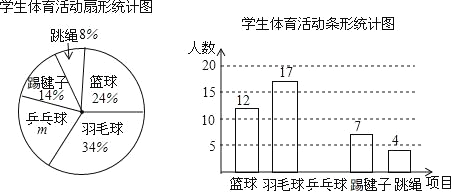
(1)m= %,這次共抽取了 名學生進行調查;并補全條形圖;
(2)請你估計該校約有 名學生喜愛打籃球;
(3)現學校準備從喜歡跳繩活動的4人(三男一女)中隨機選取2人進行體能測試,請利用列表或畫樹狀圖的方法,求抽到一男一女學生的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() .
.

(1)若BC=7,BD=4,則點![]() 到
到![]() 的距離是________;
的距離是________;
(2)若![]() ,點
,點![]() 到
到![]() 的距離是8,則
的距離是8,則![]() 的長是________.
的長是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于實數a,我們規定:用符號[![]() ]表示不大于
]表示不大于![]() 的最大整數,稱[
的最大整數,稱[![]() ]為a的根整數,例如:[
]為a的根整數,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法計算:[![]() ]= ;[
]= ;[![]() ]= .
]= .
(2)若[![]() ]=1,寫出滿足題意的x的整數值 .
]=1,寫出滿足題意的x的整數值 .
(3)如果我們對a連續求根整數,直到結果為1為止.例如:對10連續求根整數2次[![]() ]=3→[
]=3→[![]() ]=1,這時候結果為1.對145連續求根整數, 次之后結果為1.
]=1,這時候結果為1.對145連續求根整數, 次之后結果為1.
查看答案和解析>>
科目:初中數學 來源: 題型:
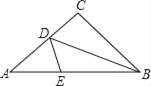
【題目】如圖,三角形紙牌中,AB=8cm,BC=6cm,AC=5cm,沿著過△ABC的頂點B的直線折疊這個三角形,使點C落在AB邊上的點E處,折痕為BD,則△AED周長為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B、C、D、E在同一條直線上,已知AB = FC,AD = FE, BC=DE.
(1)求證:△ABD≌△FCE.
(2)AB與FC的位置關系是_________(請直接寫出結論)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上的點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 到點
到點![]() 、點
、點![]() 的距離相等,動點
的距離相等,動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿數軸向右勻速運動,設運動時間為
個單位長度的速度沿數軸向右勻速運動,設運動時間為![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)點![]() 表示的數是______.
表示的數是______.
(2)求當![]() 等于多少秒時,點
等于多少秒時,點![]() 到達點
到達點![]() 處?
處?
(3)點![]() 表示的數是______(用含字母
表示的數是______(用含字母![]() 的式子表示)
的式子表示)
(4)求當![]() 等于多少秒時,
等于多少秒時,![]() 、
、![]() 之間的距離為
之間的距離為![]() 個單位長度.
個單位長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com